题目内容
求函数f(x)=2x2-2ax+3在区间[-1,1]上的最小值.
解:f(x)=2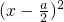 +3-
+3- .
.
(1)当 <-1,即a<-2时,函数在区间[-1,1]上单调增,
<-1,即a<-2时,函数在区间[-1,1]上单调增,
∴函数f(x)的最小值为f(-1)=5+2a;
(2)当-1≤ ≤1,即-2≤a≤2时,函数在区间[-1,
≤1,即-2≤a≤2时,函数在区间[-1, ]上单调减,在区间[
]上单调减,在区间[ ,1]上单调增,
,1]上单调增,
∴f(x)的最小值为 =3-
=3- ;
;
(3)当 >1,即a>2时,函数在区间[-1,1]上单调减,
>1,即a>2时,函数在区间[-1,1]上单调减,
∴f(x)的最小值为f(1)=5-2a.
综上可知,f(x)的最小值为
分析:先将函数配方,确定函数的对称轴,再利用对称轴与区间的位置关系,进行分类讨论,从而可求函数f(x)=2x2-2ax+3在区间[-1,1]上的最小值
点评:本题重点考查二次函数在指定区间上的最值问题,解题的关键是正确配方,确定函数的对称轴,利用对称轴与区间的位置关系,进行分类讨论.
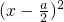 +3-
+3- .
.(1)当
 <-1,即a<-2时,函数在区间[-1,1]上单调增,
<-1,即a<-2时,函数在区间[-1,1]上单调增,∴函数f(x)的最小值为f(-1)=5+2a;
(2)当-1≤
 ≤1,即-2≤a≤2时,函数在区间[-1,
≤1,即-2≤a≤2时,函数在区间[-1, ]上单调减,在区间[
]上单调减,在区间[ ,1]上单调增,
,1]上单调增,∴f(x)的最小值为
 =3-
=3- ;
;(3)当
 >1,即a>2时,函数在区间[-1,1]上单调减,
>1,即a>2时,函数在区间[-1,1]上单调减,∴f(x)的最小值为f(1)=5-2a.
综上可知,f(x)的最小值为

分析:先将函数配方,确定函数的对称轴,再利用对称轴与区间的位置关系,进行分类讨论,从而可求函数f(x)=2x2-2ax+3在区间[-1,1]上的最小值
点评:本题重点考查二次函数在指定区间上的最值问题,解题的关键是正确配方,确定函数的对称轴,利用对称轴与区间的位置关系,进行分类讨论.

练习册系列答案
相关题目
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)