题目内容
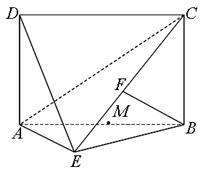
(本小题满分14分)如图,四边形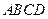 为矩形,
为矩形,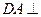 平面
平面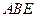 ,
,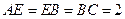 ,
,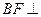 平面
平面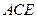 于点
于点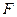 ,且点
,且点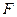 在
在 上,点
上,点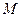 是线段
是线段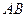 的中点。
的中点。
(1)求证: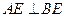 ;
;
(2)求三棱锥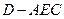 的体积;
的体积;
(3) 试在线段
试在线段 上确定一点
上确定一点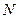 ,使得
,使得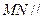 平面
平面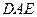 。
。
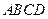 为矩形,
为矩形,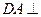 平面
平面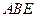 ,
,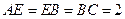 ,
,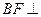 平面
平面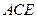 于点
于点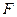 ,且点
,且点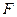 在
在 上,点
上,点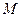 是线段
是线段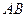 的中点。
的中点。(1)求证:
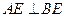 ;
;(2)求三棱锥
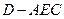 的体积;
的体积;(3)
 试在线段
试在线段 上确定一点
上确定一点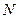 ,使得
,使得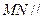 平面
平面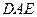 。
。
解:(1)证明:由 平面
平面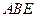 及
及

∴ 平面
平面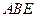 ,∴
,∴ ……………………2分
……………………2分
而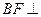 平面
平面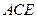 ,∴
,∴ ,又
,又 ,
,
∴ 平面
平面 ,又
,又 平面
平面 ,∴
,∴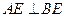 。 ……………………5分
。 ……………………5分
(2)连接 ,
, 为
为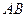 中点,
中点,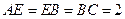 ,∴
,∴
又 平面
平面
 平面,∴
平面,∴ ,
,
所以 平面
平面 …………………………………………………………7分
…………………………………………………………7分
由已知及(1)得 .
.
故 …………………………………9分
…………………………………9分
(3)取 中点
中点 ,连接
,连接 。
。
∵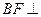 平面
平面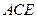 ,∴
,∴ ,
,
又 ,所以
,所以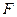 为
为 中点,
中点,
又∵ ,∴
,∴
所以 平面
平面 ……………………11分
……………………11分
同理 平面
平面 ,所以平面
,所以平面 //平面
//平面
又 平面
平面 ,则
,则 平面
平面 。 ……………………………………13分
。 ……………………………………13分
∴当点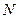 与点
与点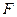 重合,即
重合,即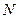 为线段
为线段 的中
的中 点时,
点时,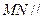 平面
平面 。………14分
。………14分
 平面
平面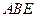 及
及

∴
 平面
平面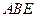 ,∴
,∴ ……………………2分
……………………2分而
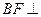 平面
平面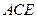 ,∴
,∴ ,又
,又 ,
,∴
 平面
平面 ,又
,又 平面
平面 ,∴
,∴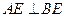 。 ……………………5分
。 ……………………5分(2)连接
 ,
, 为
为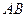 中点,
中点,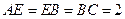 ,∴
,∴
又
 平面
平面
 平面,∴
平面,∴ ,
,所以
 平面
平面 …………………………………………………………7分
…………………………………………………………7分由已知及(1)得
 .
. 故
 …………………………………9分
…………………………………9分(3)取
 中点
中点 ,连接
,连接 。
。∵
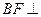 平面
平面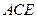 ,∴
,∴ ,
,又
 ,所以
,所以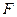 为
为 中点,
中点,
又∵
 ,∴
,∴
所以
 平面
平面 ……………………11分
……………………11分同理
 平面
平面 ,所以平面
,所以平面 //平面
//平面
又
 平面
平面 ,则
,则 平面
平面 。 ……………………………………13分
。 ……………………………………13分∴当点
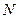 与点
与点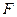 重合,即
重合,即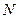 为线段
为线段 的中
的中 点时,
点时,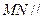 平面
平面 。………14分
。………14分略

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
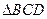 中,
中, ,
, ,
, 且
且
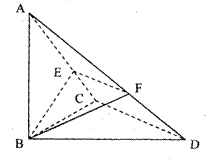
 为何值,总有
为何值,总有
 求三棱锥
求三棱锥 的体积.
的体积. 侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.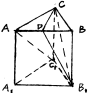
 中,
中, 、
、 分别为
分别为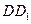 、
、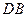 的中点. (1)求证: (1)、
的中点. (1)求证: (1)、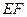 //平面
//平面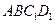 ;
;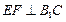 ;
;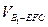 的体积.
的体积. BC,E、F分别为棱AB、PC的中点。
BC,E、F分别为棱AB、PC的中点。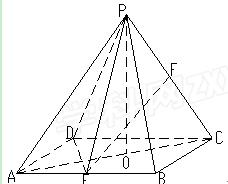
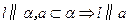
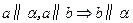
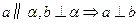
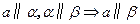
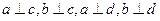 ,那么
,那么 ,
,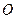 是底
是底 对角线的交点.
对角线的交点.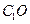 ∥面
∥面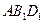 ;
; 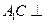 面
面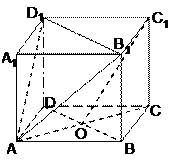
 面ABCD,
面ABCD,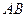 ∥
∥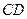 ,AD=CD=1,∠
,AD=CD=1,∠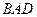 =120°,
=120°,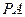 =
=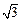 ,∠
,∠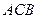 =90°,M是线段PD上的一点(不包括端点).
=90°,M是线段PD上的一点(不包括端点).