题目内容
求z=x2+y2的最大值和最小值,使式中的x、y满足约束条件
解:已知不等式组为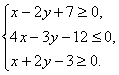
在同一直角坐标系中,作直线x-2y+7=0,4x-3y-12=0和x+2y-3=0,再根据不等式组确定可行域△ABC(如下图).
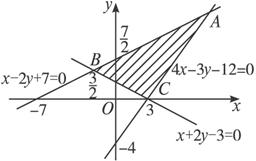
由![]() 解得点A的坐标为(5,6).
解得点A的坐标为(5,6).
所以(x2+y2)max=|OA|2=52+62=61.
因为原点O到直线BC的距离为![]() ,所以(x2+y2)min=
,所以(x2+y2)min=![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
题目内容
求z=x2+y2的最大值和最小值,使式中的x、y满足约束条件
解:已知不等式组为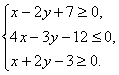
在同一直角坐标系中,作直线x-2y+7=0,4x-3y-12=0和x+2y-3=0,再根据不等式组确定可行域△ABC(如下图).

由![]() 解得点A的坐标为(5,6).
解得点A的坐标为(5,6).
所以(x2+y2)max=|OA|2=52+62=61.
因为原点O到直线BC的距离为![]() ,所以(x2+y2)min=
,所以(x2+y2)min=![]() .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案