题目内容
已知实数x,y满足 .
.(1)求z=2x+y的最小值和最大值;
(2)求
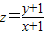 的取值范围;
的取值范围;(3)求z=x2+y2的最小值;
(4)求z=|x+y+1|最小值.
【答案】分析:(1)作出题中不等式组表示的平面区域,得到如图的△ABC及其内部.再作出直线l:z=2x+y,并将l进行平移,可得当x=y=1时,z达到最小值3;当x=5且y=2时,z达到最大值12;
(2)目标函数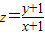 表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率,结合图形加以观察,可得z的最小值为
表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率,结合图形加以观察,可得z的最小值为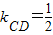 ,最大值为
,最大值为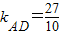 ,由此即可得到
,由此即可得到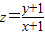 的取值范围;
的取值范围;
(3)根据两点间的距离公式,可得z=x2+y2表示可行域内一点(x,y)与原点距离的平方.结合图形加以观察,可得z=x2+y2的最小值为|BO|2=2;
(4)根据点到直线的距离公式,设d=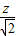 =
=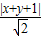 表示可行域内一点(x,y)到直线x+y+1=0的距离.观察图形可得当可行域内点与B重合时,d达到最小值,由此即可算出z=|x+y+1|最小值为3.
表示可行域内一点(x,y)到直线x+y+1=0的距离.观察图形可得当可行域内点与B重合时,d达到最小值,由此即可算出z=|x+y+1|最小值为3.
解答:解:∵实数x,y满足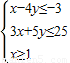
∴作出可行域,得到△ABC及其内部.其中A(1,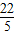 ),B(1,1),C(5,2),如图所示
),B(1,1),C(5,2),如图所示
(1)作出直线l:z=2x+y,并将l进行平移,可得
当l经过点B时,z达到最小值;当l经过点C时,z达到最大值;
∴Zmin=2×1+1=3,Zmax=2×5+2=12
即z=2x+y的最小值和最大值分别为3,12.…(3分)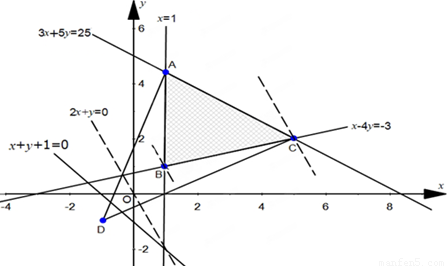
(2)∵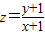 =
=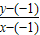 表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率
表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率
∴由图可知kCD≤z≤kAD
∵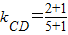 =
= ,
,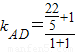 =
=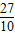
∴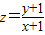 的取值范围是[
的取值范围是[ ,
,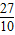 ].…(6分)
].…(6分)
(3)∵z=x2+y2表示可行域内一点(x,y)与原点距离的平方
∴由图可知当点(x,y)与B重合时,到原点的距离最小,z=x2+y2同时取到最小值
∵|BO|=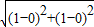 =
=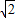
∴z=x2+y2的最小值为|BO|2=2;.…(9分)
(4)∵z=|x+y+1|,
∴d=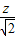 =
=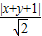 表示可行域内一点(x,y)到直线x+y+1=0的距离
表示可行域内一点(x,y)到直线x+y+1=0的距离
因此作出直线x+y+1=0,由图可知可行域内的点B到该直线的距离最小
∴点B到直线x+y+1=0的距离d=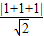 =
=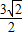 ,
,
可得可行域内的点到直线x+y+1=0的距离最小值为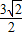
因此,zmin=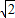 d=3,即z=|x+y+1|最小值为3.…(12分)
d=3,即z=|x+y+1|最小值为3.…(12分)
点评:本题给出二元一次不等式组表示的平面区域,求几个目标函数的最值和取值范围.着重考查了平面内两点的距离公式、点到直线的距离公式和简单的线性规划等知识点,属于中档题.
(2)目标函数
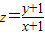 表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率,结合图形加以观察,可得z的最小值为
表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率,结合图形加以观察,可得z的最小值为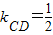 ,最大值为
,最大值为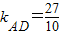 ,由此即可得到
,由此即可得到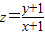 的取值范围;
的取值范围;(3)根据两点间的距离公式,可得z=x2+y2表示可行域内一点(x,y)与原点距离的平方.结合图形加以观察,可得z=x2+y2的最小值为|BO|2=2;
(4)根据点到直线的距离公式,设d=
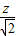 =
=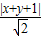 表示可行域内一点(x,y)到直线x+y+1=0的距离.观察图形可得当可行域内点与B重合时,d达到最小值,由此即可算出z=|x+y+1|最小值为3.
表示可行域内一点(x,y)到直线x+y+1=0的距离.观察图形可得当可行域内点与B重合时,d达到最小值,由此即可算出z=|x+y+1|最小值为3.解答:解:∵实数x,y满足
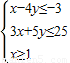
∴作出可行域,得到△ABC及其内部.其中A(1,
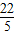 ),B(1,1),C(5,2),如图所示
),B(1,1),C(5,2),如图所示(1)作出直线l:z=2x+y,并将l进行平移,可得
当l经过点B时,z达到最小值;当l经过点C时,z达到最大值;
∴Zmin=2×1+1=3,Zmax=2×5+2=12
即z=2x+y的最小值和最大值分别为3,12.…(3分)

(2)∵
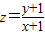 =
=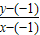 表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率
表示可行域内一点(x,y)与定点D(-1,-1)连线的斜率∴由图可知kCD≤z≤kAD
∵
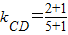 =
= ,
,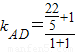 =
=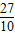
∴
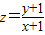 的取值范围是[
的取值范围是[ ,
,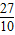 ].…(6分)
].…(6分)(3)∵z=x2+y2表示可行域内一点(x,y)与原点距离的平方
∴由图可知当点(x,y)与B重合时,到原点的距离最小,z=x2+y2同时取到最小值
∵|BO|=
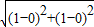 =
=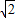
∴z=x2+y2的最小值为|BO|2=2;.…(9分)
(4)∵z=|x+y+1|,
∴d=
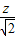 =
=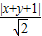 表示可行域内一点(x,y)到直线x+y+1=0的距离
表示可行域内一点(x,y)到直线x+y+1=0的距离因此作出直线x+y+1=0,由图可知可行域内的点B到该直线的距离最小
∴点B到直线x+y+1=0的距离d=
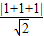 =
=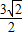 ,
,可得可行域内的点到直线x+y+1=0的距离最小值为
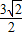
因此,zmin=
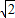 d=3,即z=|x+y+1|最小值为3.…(12分)
d=3,即z=|x+y+1|最小值为3.…(12分)点评:本题给出二元一次不等式组表示的平面区域,求几个目标函数的最值和取值范围.着重考查了平面内两点的距离公式、点到直线的距离公式和简单的线性规划等知识点,属于中档题.

练习册系列答案
相关题目