题目内容
数列{xn}由下列条件确定:x1=a>0,xn+1= ,n∈N,
,n∈N,
(Ⅰ)证明:对n≥2,总有xn≥ ;
;
(Ⅱ)证明:对n≥2,总有xn≥xn+1;
(Ⅲ)若数列{xn}的极限存在,且大于零,求 的值。
的值。
 ,n∈N,
,n∈N, (Ⅰ)证明:对n≥2,总有xn≥
 ;
;(Ⅱ)证明:对n≥2,总有xn≥xn+1;
(Ⅲ)若数列{xn}的极限存在,且大于零,求
 的值。
的值。(Ⅰ)证明:由 ,可归纳证明
,可归纳证明 ,
,
从而有 ,
,
所以,当n≥2时, 成立;
成立;
(Ⅱ)证明:当n≥2时,因为 ,
,
所以 ,
,
故当n≥2时, 成立;
成立;
(Ⅲ)解:记 且A>0,
且A>0,
由 得
得 ,
,
即 ,
,
由A>0,解得 ,
,
故 。
。
 ,可归纳证明
,可归纳证明 ,
,从而有
 ,
,所以,当n≥2时,
 成立;
成立;(Ⅱ)证明:当n≥2时,因为
 ,
,所以
 ,
,故当n≥2时,
 成立;
成立;(Ⅲ)解:记
 且A>0,
且A>0,由
 得
得 ,
,即
 ,
,由A>0,解得
 ,
,故
 。
。 
练习册系列答案
相关题目
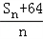 的最小值;
的最小值;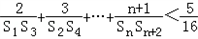 ;
; 的最小值是
的最小值是
 的最小值是( )
的最小值是( ) =(x﹣1,2),
=(x﹣1,2), =(4,y),若
=(4,y),若 ⊥
⊥ ,则9x+3y的最小值为( )。
,则9x+3y的最小值为( )。 的最大值为
的最大值为