题目内容
10.函数f(x)=($\frac{2}{1+{e}^{x}}$-1)cosx的图象的大致形状是( )| A. | 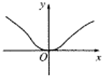 | B. |  | C. | 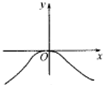 | D. | 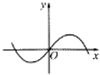 |
分析 分析函数奇偶性和x∈(0,$\frac{π}{2}$)时函数图象的位置,排除错误答案,可得结论.
解答 解:∵f(x)=($\frac{2}{1+{e}^{x}}$-1)cosx,
∴f(-x)=($\frac{2}{1+{e}^{-x}}$-1)cos(-x)=($\frac{{2e}^{x}}{1+{e}^{x}}$-1)cosx=-($\frac{2}{1+{e}^{x}}$-1)cosx=-f(x),
故函数f(x)为奇函数,故函数图象关于原点对称,可排除A,C,
又由当x∈(0,$\frac{π}{2}$),f(x)<0,函数图象位于第四象限,可排除D,
故选:B
点评 本题考查的知识点是函数的图象,由于函数非基本初等函数,故利用排除法,是解答的最佳选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.点(1,1)在不等式组$\left\{\begin{array}{l}{mx+ny≤2}\\{ny-mx≤2}\\{ny≥1}\end{array}\right.$表示的平面区域内,则m2+n2取值范围是( )
| A. | [1,4] | B. | [2,4] | C. | [1,3] | D. | [2,3] |
15.a∈R,则“a=1”是“直线ax-y+2=0与直线x-ay-1=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.记<n>表示正整数n的个位数,设Sn为数列{an}的前n项和,若an=<n2>,则Sn的值不可能为( )
| A. | 4500 | B. | 4505 | C. | 4514 | D. | 4519 |