题目内容
20.△ABC的三内角A,B,C 所对边长分别为a,b,c,a2-b2=bc,AD为角A的平分线,且△ACD与△ABD面积之比为1:2.(1)求角A的大小;
(2)若 AD=$\sqrt{3}$,求△ABC的面积.
分析 (1)由a2-b2=bc得$\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{bc+{c^2}}}{2ac}$,由正弦及余弦定理化简整理可得A=2B,由AD为角A的平分线,且S△ACD:S△ABD=1:2,解得$c=2b,a=\sqrt{3}b$,由正弦定理可得cosB,即可求得B,A的值.
(2)由已知可求BD,CD,AC,根据三角形面积公式即可得解.
解答 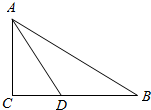 (本题满分为12分)
(本题满分为12分)
解:(1)由a2-b2=bc得$\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{bc+{c^2}}}{2ac}$,
由正弦及余弦定理得:$cosB=\frac{sinB+sinC}{2sinA}$,…(2分)
可得:2sinAcosB=sinB+sin(A+B),
整理得sin(A-B)=sinB,即A=2B,…(4分)
因为AD为角A的平分线,且S△ACD:S△ABD=1:2,
所以$c=2b,a=\sqrt{3}b$,
所以$sinA=\sqrt{3}sinB$,…(6分)$⇒sin2B=\sqrt{3}sinB⇒cosB=\frac{{\sqrt{3}}}{2}$即$B=\frac{π}{6},A=\frac{π}{3}$…(8分)
(2)∵$AD=\sqrt{3}$
所以$AD=BD=\sqrt{3},CD=\frac{{\sqrt{3}}}{2},AC=\frac{3}{2}$,…(10分)
∴${S_{△ABC}}=\frac{1}{2}×\frac{{3\sqrt{3}}}{2}×\frac{3}{2}=\frac{{9\sqrt{3}}}{8}$. …(12分)
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式在解三角形中的综合应用,考查了计算能力,熟练掌握和灵活应用相关公式定理是解题的关键,属于基本知识的考查.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
| A. | ($\frac{1}{10}$,1) | B. | (0,$\frac{1}{10}$)∪(10,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,1)∪(10,+∞) |
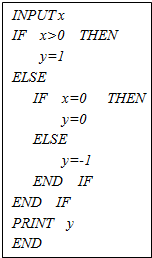 读程序,回答下列问题:
读程序,回答下列问题: