题目内容
已知a<b,则下列不等式正确的是
- A.
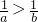
- B.a2>b2
- C.2-a>2-b
- D.2a>2b
C
分析:不妨令a=-1且 b=1,可得A、B、D不成立,而 C成立,由此得出结论.
解答:不妨令a=-1且 b=1,可得 ,故A 不成立.
,故A 不成立.
可得a2=1,b2=1,故B 不成立.
可得 2-a=3,2-b=1,故有 2-a>2-b,故C成立.
(证明:∵a<b,∴-a>-b,∴2-a>2-b ).
由于函数y=2x 在R上是增函数,∴2a<2b,故D不成立.
故选C.
点评:本题主要考查不等式与不等关系,不等式的基本性质,利用特殊值代入法,排除不符合条件的选项,得到符合条件的选项,是一种简单有效的方法.
分析:不妨令a=-1且 b=1,可得A、B、D不成立,而 C成立,由此得出结论.
解答:不妨令a=-1且 b=1,可得
 ,故A 不成立.
,故A 不成立.可得a2=1,b2=1,故B 不成立.
可得 2-a=3,2-b=1,故有 2-a>2-b,故C成立.
(证明:∵a<b,∴-a>-b,∴2-a>2-b ).
由于函数y=2x 在R上是增函数,∴2a<2b,故D不成立.
故选C.
点评:本题主要考查不等式与不等关系,不等式的基本性质,利用特殊值代入法,排除不符合条件的选项,得到符合条件的选项,是一种简单有效的方法.

练习册系列答案
相关题目
已知a>b,则下列不等式①a2>b2②
<
③
>
中不一定成立的个数是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-b |
| 1 |
| a |
| A、3 | B、1 | C、0 | D、2 |
 ③
③ 中不一定成立的个数是( )
中不一定成立的个数是( ) ③
③ 中不一定成立的个数是( )
中不一定成立的个数是( )