题目内容
我们把棱长要么为1cm,要么为2cm的三棱锥定义为“和谐棱锥”.在所有结构不同的“和谐棱锥”中任取一个,取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是( )
分析:分类讨论课的,存在“和谐棱锥”的可能情况共有5种,而有且仅有一个面是等边三角形的情况只有一种,由此求得所求事件的概率.
解答:解:由于三角形任意两边之和大于第三边,故共面的三边长不能为1,1,2.
故三棱锥的六条棱的长度存在以下几种情况:①六个1;②五个1和一个2,这样不可以,因为有的面不能构成三角形,故不能构成三棱锥;
③四个1和两个2,这样不可以,因为有的面不能构成三角形,故不能构成三棱锥;
④三个1和三个2;⑤两个1和4个2;⑥一个1和5个2;⑦六个2.
显然,存在的可能情况共有5种,而有且仅有一个面是等边三角形的情况只有④,
故取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是
,
故选D.
故三棱锥的六条棱的长度存在以下几种情况:①六个1;②五个1和一个2,这样不可以,因为有的面不能构成三角形,故不能构成三棱锥;
③四个1和两个2,这样不可以,因为有的面不能构成三角形,故不能构成三棱锥;
④三个1和三个2;⑤两个1和4个2;⑥一个1和5个2;⑦六个2.
显然,存在的可能情况共有5种,而有且仅有一个面是等边三角形的情况只有④,
故取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是
| 1 |
| 5 |
故选D.
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
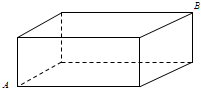 蚂蚁搬家都选择最短路线行走,有一只蚂蚁沿棱长分别为1cm,2cm,3cm的长方体木块的顶点A处沿表面达到顶点B处(如图所示),这只蚂蚁走的路程是( )
蚂蚁搬家都选择最短路线行走,有一只蚂蚁沿棱长分别为1cm,2cm,3cm的长方体木块的顶点A处沿表面达到顶点B处(如图所示),这只蚂蚁走的路程是( )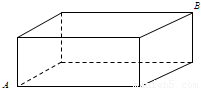
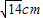
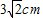
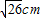
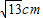





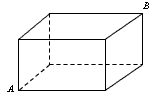
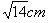
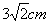
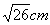
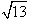 cm
cm