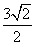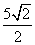题目内容
已知x,y都是正实数,且x+y-3xy+5=0.
(1)求xy的最小值;
(2)求x+y的最小值.
解析:(1)由x+y-3xy+5=0,得x+y+5=3xy.
∴2+5≤x+y+5=3xy.
∴3xy-2-5≥0.
∴(+1)(3-5)≥0.
∴≥ ,
, 即xy≥
即xy≥ ,等号成立的条件是x=y.
,等号成立的条件是x=y.
此时x=y= ,故xy的最小值是
,故xy的最小值是 .
.
(2)方法一:∵x+y+5=3xy≤3· 2=
2= (x+y)2,
(x+y)2,
∴ (x+y)2-(x+y)-5≥0.
(x+y)2-(x+y)-5≥0.
即3(x+y)2-4(x+y)-2 0≥0.
0≥0.
即[(x+y)+2][3(x+y)-10]≥0.
∴x+y≥ .
.
等号成立的条件是x=y,即x=y= 时取得.
时取得.
故x+y的最小值为 .
.
方法二:由(1)知,x+y+5=3xy,且(xy)min= ,
,
∴3(xy)min= .
.
∴(x+y)min= -5=
-5= ,此时x=y=
,此时x=y= .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 则使得
则使得 的自变量x的取值范围为( )
的自变量x的取值范围为( ) 中,
中, 是斜边
是斜边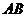 上的高,则下列等式中不成立的是 ( ).
上的高,则下列等式中不成立的是 ( ). B.
B.
 D.
D.

 的离心率为
的离心率为 ,则
,则 的渐近线方程为( )
的渐近线方程为( ) B.
B. C.
C. D.
D.
 ,若
,若 中元素至多只有一个,求
中元素至多只有一个,求 的取值范围__________.
的取值范围__________. 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( ).
轴相切,则该圆的标准方程是( ). B.
B.
 D.
D.
 ,当
,当 变化时所得的直线都经过的定点为____________.
变化时所得的直线都经过的定点为____________. 且与
且与 有相同焦点的椭圆的方程是
有相同焦点的椭圆的方程是 B.
B. C.
C. D.
D.
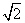 围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=
围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=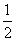 x-y的最小值为( )
x-y的最小值为( )