题目内容

20．如果1≤x≤2．求y=$\frac{2x+1}{x+1}$的取值范围．

分析 把已知的函数解析式变形，画出图形，可知函数求y=$\frac{2x+1}{x+1}$在[1，2]上为增函数，由单调性求得函数的值域．

解答 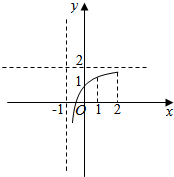解：∵y=$\frac{2x+1}{x+1}$=$\frac{2（x+1）-1}{x+1}=-\frac{1}{x+1}+2$，
又1≤x≤2，
如图：
由图可知，函数求y=$\frac{2x+1}{x+1}$在[1，2]上为增函数，
∴当x=1时，函数取得最小值$\frac{3}{2}$，当x=2时，函数取得最大值$\frac{5}{3}$．
故答案为[$\frac{3}{2}，\frac{5}{3}$]．

点评 本题考查函数的值域的求法，考查了数形结合的解题思想方法，是中档题．

练习册系列答案
相关题目
10．已知函数y=f（x）的定义域为R，且不恒为0，且对任意x，y∈R，都有f（x+y）=f（x）+f（y）．
（1）求f（0）的值；
（2）判断函数y=f（x）的奇偶性；
（3）当x＞0时，f（x）＜0，判断函数y=f（x）的单调性．
11．已知集合A={x∈R|log2（x-1）＜2}，B={x∈R||3x-b|＜4}．
（Ⅰ）若A∪B=A，求实数b的取值范围；
（Ⅱ）若集合B∩N*={1，2，3}，求实数b的取值范围．
8．若向量$\overrightarrow{OP}$=（3+t）$\overrightarrow{i}$+（1+2t）$\overrightarrow{j}$．则|$\overrightarrow{OP}$|的最小值为$\sqrt{5}$．
15．已知函数f（x）=$\left\{\begin{array}{l}{2，x∉[-2，2]}\\{|x|，x∈[-2，2]}\end{array}\right.$，则其最小值为（　　）
A．2B．0C．-2D．不存在
5．已知函数f（x）=sin（x+$\frac{π}{6}$）cos（x+$\frac{π}{3}$），求函数g（x）=f（x）+sinx在区间[-$\frac{π}{6}$，$\frac{2π}{3}$]上的值域．
12．设函数f（x）是定义在R上的增函数，如果不等式f（ax2+x-2）＜f（x2-x+1）对于任意x∈[$\frac{3}{2}$，+∞）恒成立，求实数a的取值范围．
13．求函数f（x）=cos2x-3sin2x的最小正周期．
14．已知函数f（x）=ex-mx-exlnx+1，且定义域为（0，e]，若函数f（x）在定义域内有两个极值点，则m的取值范围为（　　）
A．[0，ee-2e]B．（0，ee-2e]C．（0，ee-2e）D．（ee-2e，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网