题目内容
已知数列{an}各项均为正数,其前n项和Sn满足2Sn=an2+an(n∈N*)。
(Ⅰ)证明:{an}为等差数列;
(Ⅱ)令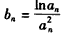 ,记{bn}的前n项和为Tn,求证:
,记{bn}的前n项和为Tn,求证: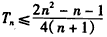 。
。
(Ⅰ)证明:{an}为等差数列;
(Ⅱ)令
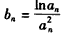 ,记{bn}的前n项和为Tn,求证:
,记{bn}的前n项和为Tn,求证: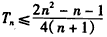 。
。 (Ⅰ)证明:∵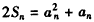 ,
,
∴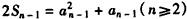 ,
,
两式相减,得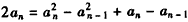 ,
,
整理,得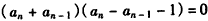 ,
,
∵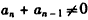 ,
,
∴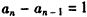 (常数),
(常数),
又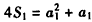 ,
,
即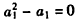 ,解得:
,解得: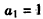 ,
,
∴{an}是以1为首项,1为公差的等差数列。
(Ⅱ)解:由(Ⅰ)知,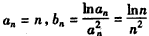 ,
,
即证: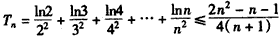 ,
,
设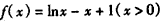 ,
,
则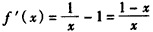 ,
,
当x∈(0,1),f′(x)>0,f(x)为单调递增函数;
当x∈(1,+∞),f′(x)<0,f(x)单调递减函数;
在x=1处f(x)取得极大值,也取得最大值f(x)≤f(1)=0,即lnx-x+1≤0,
∴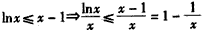 ,
,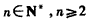 时,令
时,令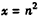 ,得
,得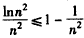 ,
,
∴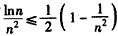 ,
,
∴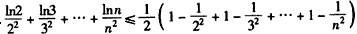
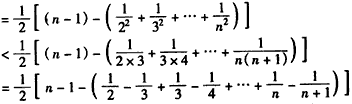
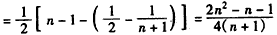 ,
,
∴当n=1时,有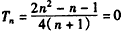 。
。
故结论成立。

练习册系列答案
相关题目
