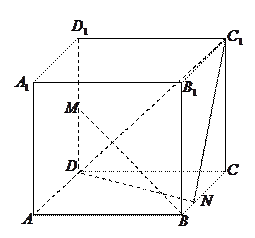题目内容
(本题满分14分)
如图,在正方体ABCD—A1B1C1D1中,M、N、G
分别是A1A,D1C,AD的中点.求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.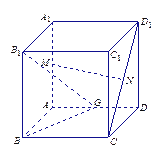
如图,在正方体ABCD—A1B1C1D1中,M、N、G
分别是A1A,D1C,AD的中点.求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.

略
证明:(1)取CD的中点记为E,连NE,AE.
由N,E分别为CD1与CD的中点可得
NE∥D1D且NE=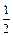 D1D, ………………………………2分
D1D, ………………………………2分
又AM∥D1D且AM=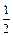 D1D………………………………4分
D1D………………………………4分
所以AM∥EN且AM=EN,即四边形AMNE为平行四边形
所以MN∥AE, ………………………………6分
又AE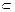 面ABCD,所以MN∥面ABCD……8分
面ABCD,所以MN∥面ABCD……8分
(2)由AG=DE ,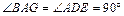 ,DA=AB
,DA=AB
可得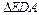 与
与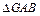 全等……………………………10分
全等……………………………10分
所以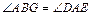 , ……………………………………………11分
, ……………………………………………11分
又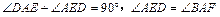 ,所以
,所以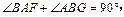
所以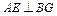 , ………………………………………………12分
, ………………………………………………12分
又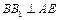 ,所以
,所以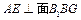 , ……………………………………………………13分
, ……………………………………………………13分
又MN∥AE,所以MN⊥平面B1BG ……………………………………………14分
由N,E分别为CD1与CD的中点可得
NE∥D1D且NE=
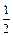 D1D, ………………………………2分
D1D, ………………………………2分又AM∥D1D且AM=
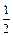 D1D………………………………4分
D1D………………………………4分所以AM∥EN且AM=EN,即四边形AMNE为平行四边形
所以MN∥AE, ………………………………6分
又AE
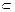 面ABCD,所以MN∥面ABCD……8分
面ABCD,所以MN∥面ABCD……8分(2)由AG=DE ,
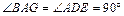 ,DA=AB
,DA=AB可得
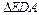 与
与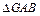 全等……………………………10分
全等……………………………10分所以
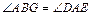 , ……………………………………………11分
, ……………………………………………11分又
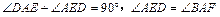 ,所以
,所以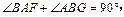
所以
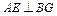 , ………………………………………………12分
, ………………………………………………12分又
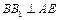 ,所以
,所以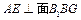 , ……………………………………………………13分
, ……………………………………………………13分又MN∥AE,所以MN⊥平面B1BG ……………………………………………14分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
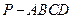 的底面为直角梯形,
的底面为直角梯形, ,
,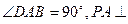 底面
底面 ,且
,且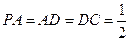 ,
, ,
, 是
是 的中点。
的中点。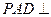 面
面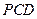 ;
;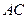 与
与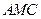 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.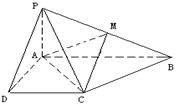
 .
.
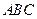 的边长为4,
的边长为4,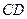 是
是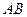 边上的高,
边上的高,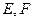 分别是
分别是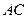 和
和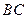 边的中点,现将△
边的中点,现将△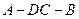 .
.
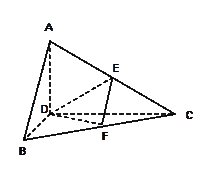
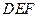 的位置关系,并说明理由;
的位置关系,并说明理由;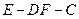 的余弦值;
的余弦值;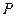 ,使
,使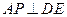 ?证明你的结论.
?证明你的结论.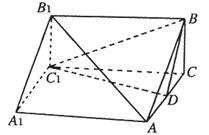
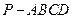 中,底面
中,底面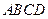 是矩形,
是矩形,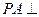 平面
平面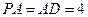 ,
,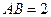 . 以
. 以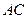 的中点
的中点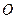 为球心、
为球心、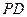 于点
于点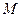 ,交
,交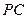 于点
于点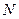 .
.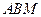 ⊥平面
⊥平面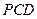 ;
;
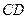 与平面
与平面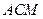 所成的角的正弦值.
所成的角的正弦值.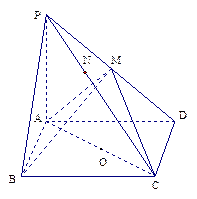
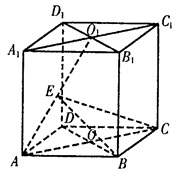
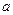 的正方体ABCD—A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点。
的正方体ABCD—A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点。
 ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=
ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=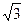 ,D是线段A1B1的中点.
,D是线段A1B1的中点. 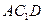 ⊥平面A1B1BA;
⊥平面A1B1BA;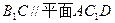 ;
;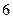 的正方体
的正方体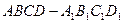 中,
中,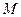 是
是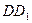 的中点,
的中点,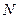 在线段
在线段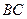 上,且
上,且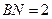 .
.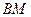 与
与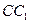 所成角的余弦值;
所成角的余弦值;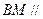 面
面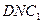 ;
;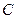 到面
到面