题目内容
设 ,
, ,
, 是两两不共线的向量,下列命题中不正确的是
是两两不共线的向量,下列命题中不正确的是
- A.

- B.一定存在实数λ1,λ2,使得

- C.若
 ,则必有λ1=u1且λ2=u2
,则必有λ1=u1且λ2=u2 - D.

D
分析:A:由向量加法的多边形法则可判断B:由平面向量的基本定理可判断:由已知可得 ,结合
,结合 不共线可得λ1=μ1λ,2=μ2,D:由于
不共线可得λ1=μ1λ,2=μ2,D:由于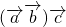 与
与 共线的向量,而
共线的向量,而 表示与
表示与 共线的向量且
共线的向量且 不共线
不共线
解答:设
A: =
=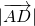
 ,故A正确
,故A正确
B:由平面向量的基本定理可得B正确
C:由 ,可得
,可得 ,由
,由 不共线可得λ1=μ1λ,2=μ2,故C正确
不共线可得λ1=μ1λ,2=μ2,故C正确
D:由于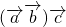 与
与 共线的向量,而
共线的向量,而 表示与
表示与 共线的向量且
共线的向量且 不共线,故D错误
不共线,故D错误
故选:D
点评:本题主要考查了向量加法的多边形法则、向量共线定理、平面向量的基本定理及向量数量积的运算性质等知识的综合考查,解题的关键熟练掌握向量的性质并能灵活应用.
分析:A:由向量加法的多边形法则可判断B:由平面向量的基本定理可判断:由已知可得
 ,结合
,结合 不共线可得λ1=μ1λ,2=μ2,D:由于
不共线可得λ1=μ1λ,2=μ2,D:由于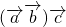 与
与 共线的向量,而
共线的向量,而 表示与
表示与 共线的向量且
共线的向量且 不共线
不共线解答:设

A:
 =
=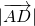
 ,故A正确
,故A正确B:由平面向量的基本定理可得B正确
C:由
 ,可得
,可得 ,由
,由 不共线可得λ1=μ1λ,2=μ2,故C正确
不共线可得λ1=μ1λ,2=μ2,故C正确D:由于
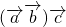 与
与 共线的向量,而
共线的向量,而 表示与
表示与 共线的向量且
共线的向量且 不共线,故D错误
不共线,故D错误故选:D
点评:本题主要考查了向量加法的多边形法则、向量共线定理、平面向量的基本定理及向量数量积的运算性质等知识的综合考查,解题的关键熟练掌握向量的性质并能灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目