题目内容
已知点A(-1,O),B(1,0),动点M的轨迹曲线C满足∠AMB=2θ,|
|•|
|cos2θ=3.
(I)求曲线C的方程;
(II)试探究曲线C上是否存在点P,使直线PA与PB的斜率kPA•kPB=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
| AM |
| BM |
(I)求曲线C的方程;
(II)试探究曲线C上是否存在点P,使直线PA与PB的斜率kPA•kPB=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
分析:(Ⅰ)设M(x,y),在△MAB中,|AB|=2,∠AMB=2θ,根据余弦定理,及|
|•|
|cos2θ=3,可得|
|+|
|=4,从而可得点M的轨迹是以A、B为焦点的椭圆(点M在x轴上也符合题意),由此可得曲线C的方程;
(Ⅱ)由(Ⅰ)知曲线C是椭圆,它的两个焦点坐标分别为A(-1,0),B(1,0),利用直线PA与PB的斜率kPA•kPB=1可得方程,根据双曲线的两个顶点在椭圆内,结合椭圆和双曲线的对称性可得结论.
| AM |
| BM |
| AM |
| BM |
(Ⅱ)由(Ⅰ)知曲线C是椭圆,它的两个焦点坐标分别为A(-1,0),B(1,0),利用直线PA与PB的斜率kPA•kPB=1可得方程,根据双曲线的两个顶点在椭圆内,结合椭圆和双曲线的对称性可得结论.
解答:解:(Ⅰ)设M(x,y),在△MAB中,|AB|=2,∠AMB=2θ,
根据余弦定理得|
|2+|
|2-2|
|•|
|cos2θ=4.…(2分)
即(|
|+|
|)2-2|
|•|
|(1+cos2θ)=4(|
|+|
|)2-4|
|•|
|cosθ=4.
而|
|•|
|cos2θ=3,所以(|
|+|
|2)-4×3=4.
所以|
|+|
|=4…(5分)
又|
|+|
|=4>2=|AB|
因此点M的轨迹是以A、B为焦点的椭圆(点M在x轴上也符合题意),所以a=2,c=1.
所以曲线C的方程为
+
=1.…(7分)
(Ⅱ)由(Ⅰ)知曲线C是椭圆,它的两个焦点坐标分别为A(-1,0),B(1,0),
设P(x,y)是椭圆上的点,
∵kPA•kPB=1,∴
•
=1(x≠±1),
∴x2-y2=1(x≠±1),…(11分)
这是实轴在x轴,顶点是椭圆的两个焦点的双曲线,它与椭圆的交点即为点P.
由于双曲线的两个顶点在椭圆内,根据椭圆和双曲线的对称性可知,它们必有四个交点.
即圆心M的轨迹上存在四个点P,使直线PA与PB的斜率kPA•kPB=1.…(14分)
根据余弦定理得|
| AM |
| BM |
| AM |
| BM |
即(|
| AM |
| BM |
| AM |
| BM |
| AM |
| BM |
| AM |
| BM |
而|
| AM |
| BM |
| AM |
| BM |
所以|
| AM |
| BM |
又|
| AM |
| BM |
因此点M的轨迹是以A、B为焦点的椭圆(点M在x轴上也符合题意),所以a=2,c=1.
所以曲线C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)由(Ⅰ)知曲线C是椭圆,它的两个焦点坐标分别为A(-1,0),B(1,0),
设P(x,y)是椭圆上的点,
∵kPA•kPB=1,∴
| y |
| x+1 |
| y |
| x-1 |
∴x2-y2=1(x≠±1),…(11分)
这是实轴在x轴,顶点是椭圆的两个焦点的双曲线,它与椭圆的交点即为点P.
由于双曲线的两个顶点在椭圆内,根据椭圆和双曲线的对称性可知,它们必有四个交点.
即圆心M的轨迹上存在四个点P,使直线PA与PB的斜率kPA•kPB=1.…(14分)
点评:本题考查向量知识的运用,考查椭圆的标准方程,考查椭圆与双曲线的对称性,正确运用向量知识是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
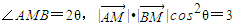 .
.