题目内容
6.双曲线$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{3}$=1的渐近线方程为( )| A. | y=±3x | B. | y=±$\sqrt{3}$x | C. | y=±x | D. | y=±$\frac{\sqrt{3}}{3}$x |
分析 利用双曲线的简单性质求解.
解答 解:双曲线$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{3}$=1的渐近线方程为$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{3}$=0,
整理,得y=±x.
故选:C.
点评 本题考查双曲线的渐近线方程的求法,是基础题,解题时要认真审题,注意双曲线性质的合理运用.

练习册系列答案
相关题目
1.执行如图所示的程序框图,则输出S的值是( )
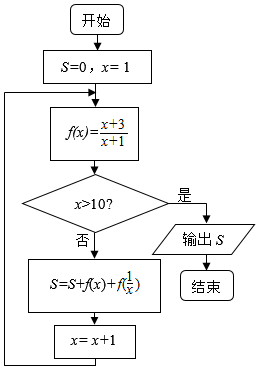

| A. | 36 | B. | 40 | C. | 44 | D. | 48 |
11.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P是椭圆上一点,|PF1|=λ|PF2|($\frac{1}{2}$≤λ≤2),∠F1PF2=$\frac{π}{2}$,则椭圆离心率的取值范围为( )
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{5}}{3}$] | C. | [$\frac{2}{3}$,$\frac{\sqrt{5}}{3}$] | D. | [$\frac{\sqrt{5}}{3}$,1) |
18.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4,则P=( )
| A. | 1 | B. | 4 | C. | 2 | D. | 8 |
16.已知U={1,2,3,4},集合A={1,4},则∁UA=( )
| A. | {2} | B. | {3} | C. | {2,3} | D. | {1,2,4} |
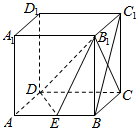 如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,
如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,