题目内容
计算
(1-
)(1-
)(1-
)…(1-
)=( )
| lim |
| n→∞ |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:数列的极限
专题:计算题
分析:直接求极限是不能求的,所以想着怎么将式子化简,可试着将式子每一项因式通分并用上平方差公式得:原式=
[
•
•
…
]=
(
)=
(
)=
.
| lim |
| n→∞ |
| 3•1 |
| 2•2 |
| 4•2 |
| 3•3 |
| 5•3 |
| 4•4 |
| (n+1)•(n-1) |
| n•n |
| lim |
| n→∞ |
| n+1 |
| 2n |
| lim |
| n→∞ |
1+
| ||
| 2 |
| 1 |
| 2 |
解答:
解:∵(1-
)(1-
)(1-
)…(1-
)=
•
•
…
=
•
•
…
=
=
;
∴原式=
=
.
故选A.
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
| 22-1 |
| 22 |
| 32-1 |
| 32 |
| 42-1 |
| 42 |
| n2-1 |
| n2 |
| 3•1 |
| 2•2 |
| 4•2 |
| 3•3 |
| 5•3 |
| 4•4 |
| (n+1)(n-1) |
| n•n |
| n+1 |
| 2n |
1+
| ||
| 2 |
∴原式=
| lim |
| n→∞ |
1+
| ||
| 2 |
| 1 |
| 2 |
故选A.
点评:考查数列极限的概念及求法,而求解本题的关键是对式子的化简.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a2+b2≠0,c2+d2≠0,
、
为相互垂直的单位向量,则向量(a
+b
)⊥向量(c
+d
)的充要条件是向量(a
+b
)∥( )
| i |
| j |
| i |
| j |
| i |
| j |
| i |
| j |
A、-c
| ||||
B、d
| ||||
C、c
| ||||
D、-d
|
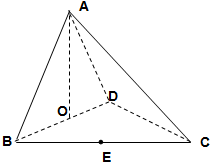 如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=