题目内容
已知函数 的最小正周期是
的最小正周期是 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)求 在[
在[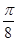 ,
, ]上的最大值和最小值.
]上的最大值和最小值.
(1)  ; (2)最大值
; (2)最大值 、最小值
、最小值
解析试题分析:(1)首先利用三角恒等变换将函数解析式 化为
化为  ,然后根据周期公式确定
,然后根据周期公式确定 的值.最后利用正弦函数的单调性求出
的值.最后利用正弦函数的单调性求出 的单调递增区间
的单调递增区间
(2)由




试题解析:
解:(1)
= 3分
3分
最小正周期是
所以, 从而
从而 5分
5分
令 ,解得
,解得 7分
7分
所以函数 的单调递增区间为
的单调递增区间为 8分
8分
(2)当 时,
时, 9分
9分 11分
11分
所以 在
在 上的最大值和最小值分别为
上的最大值和最小值分别为 、
、 . 12分
. 12分
考点:1、三角函数的恒等变换;2、函数 的性质;
的性质;

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
.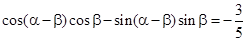 ,
, ,求
,求 的值.
的值. ,设函数
,设函数 .
. ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.
 ,
,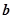
 ,且
,且
 及
及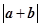

 -
-
 ,求
,求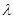 的值。.
的值。. ,且
,且 .
. ;
; .
. .
.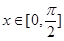 时,求
时,求 的值域;
的值域; 的内角
的内角 的对边分别为
的对边分别为 ,且满足
,且满足 ,
, ,求
,求 的值.
的值. sin Ccos C-cos2C=
sin Ccos C-cos2C= ,且c=3.
,且c=3. <α<
<α< π,cos(
π,cos( ,sin(
,sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.