题目内容
已知向量
 ,
,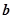
 ,且
,且
(1)求 及
及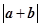
(2)若
 -
-
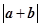 的最小值是
的最小值是 ,求
,求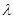 的值。.
的值。.
(1) ;(2)
;(2) 
解析试题分析:(1)由向量数量积, 向量的模长公式以及两角和的余弦、二倍角的余弦公式即可求解;
(2)以向量为载体考察三角函数知识以及二次函数在闭区间上的最值问题,体现分类讨论思想
试题解析:(1) . 1分
. 1分 .
.  ,所以
,所以 . 3分
. 3分
(2) . 4分
. 4分 ,所以
,所以 .
.
①当 时,当且仅当
时,当且仅当 时,
时, 取最小值-1,这与题设矛盾.
取最小值-1,这与题设矛盾.
②当 时,当且仅当
时,当且仅当 时,
时, 取最小值
取最小值 .由
.由 得
得 .
.
③当 时,当且仅当
时,当且仅当 时,
时, 取最小值
取最小值 .由
.由 得
得 ,故舍去..
,故舍去..
综上得: . 10分
. 10分
考点:向量数量积,向量的模长公式以及两角和的余弦、二倍角的余弦公式,二次函数在闭区间上的最值问题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.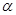 为第三象限角,
为第三象限角,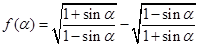 .
.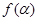 ;
;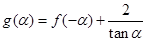 ,求函数
,求函数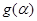 的最小值,并求取最小值时的
的最小值,并求取最小值时的
 的值,
的值, 的值.
的值. 的最小正周期是
的最小正周期是 .
. 的单调递增区间;
的单调递增区间;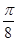 ,
, ]上的最大值和最小值.
]上的最大值和最小值. 中,内角A,B,C所对的边分别为a,b,c,且
中,内角A,B,C所对的边分别为a,b,c,且 .
. ,
, 为
为 的最大值,并指出此时B的值.
的最大值,并指出此时B的值. 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在 上的单调递增区间.
上的单调递增区间. 。
。 的单调区间;
的单调区间; =1,BC=2,B=
=1,BC=2,B= ,求AC边的长.
,求AC边的长. ,tanβ=-
,tanβ=-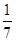 ,求2α-β的值.
,求2α-β的值.