题目内容
1.设抛物线y2=8x上有两点A,B,其焦点为F,满足$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则|AB|=9.分析 由于$\overrightarrow{AF}$=2$\overrightarrow{FB}$,可得直线经过焦点F(2,0).设A(x1,y1),B(x2,y2)(x1>x2).设直线AB的方程为:
y=k(x-2).与抛物线的方程联立可得根与系数的关系,再利用向量的坐标运算、焦点弦长公式即可得出.
解答 解:∵$\overrightarrow{AF}$=2$\overrightarrow{FB}$,∴直线经过焦点F(2,0),
设A(x1,y1),B(x2,y2)(x1>x2).
设直线AB的方程为:y=k(x-2).
与抛物线方程联立,化为k2x2-(4k2+8)x+4k2=0,
则x1+x2=$\frac{4{k}^{2}+8}{{k}^{2}}$,x1x2=4.
∵$\overrightarrow{AF}$=2$\overrightarrow{FB}$,∴x1-2+2(x2-2)=0,
∴x1+2x2=6,解得x1=4,x2=1,k2=8.
∴|AB|=x1+x2+p=5+4=9.
故答案为:9.
点评 本题考查了直线与抛物线相交转化为方程联立可得根与系数的关系、向量的坐标运算、焦点弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.过点P(3,0)有一条直线l,它夹在两条直线l1:2x-y-2=0与l2:x+y+3=0之间的线段恰被点P平分,则直线l方程为( )
| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
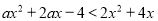 对任意实数x均成立,则实数a的取值范围是( )
对任意实数x均成立,则实数a的取值范围是( )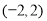 B.
B.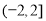
 D.
D.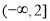
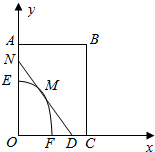 如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.
如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.