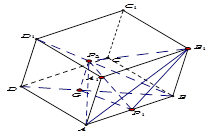
题目内容
如图,四棱锥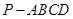 中,底面
中,底面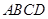 是菱形,
是菱形,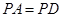 ,
,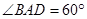 ,
,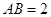 ,
,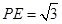 ,
,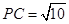 ,
,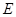 是
是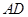 的中点,
的中点,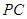 上的点
上的点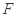 满足
满足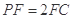 .
.

(Ⅰ)求证: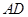
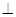 平面
平面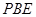 ;
;
(Ⅱ)求三棱锥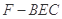 的体积.
的体积.
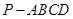 中,底面
中,底面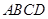 是菱形,
是菱形,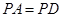 ,
,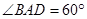 ,
,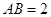 ,
,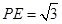 ,
,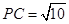 ,
,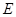 是
是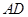 的中点,
的中点,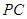 上的点
上的点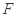 满足
满足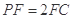 .
.
(Ⅰ)求证:
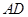
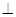 平面
平面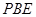 ;
;(Ⅱ)求三棱锥
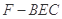 的体积.
的体积.(I)详见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)
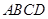 是菱形,
是菱形,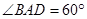 ,这是由两个正三角形
,这是由两个正三角形 构成的菱形,又
构成的菱形,又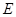 是
是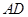 的中点,
的中点, .又
.又 ,
, .由此可得
.由此可得 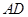
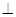 平面
平面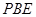 .(Ⅱ)
.(Ⅱ)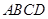 是由正三角形
是由正三角形 构成的菱形,又
构成的菱形,又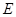 是
是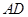 的中点,所以
的中点,所以 ,所以
,所以 .另外根据所给长度,用勾股定理可得
.另外根据所给长度,用勾股定理可得 ,又
,又 ,
, ,
, 平面
平面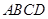 .又
.又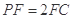 ,所以点F到平面BEC的距离等于
,所以点F到平面BEC的距离等于 ,这样由棱锥的体积公式可得
,这样由棱锥的体积公式可得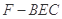 的体积.
的体积.试题解析:(Ⅰ)证明:
 ,
,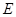 是
是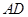 的中点,
的中点, . (2分)
. (2分) ,,
,,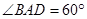 ,
, 是正三角形, (3分)
是正三角形, (3分) . (4分)
. (4分)又
 ,
,
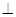 平面
平面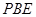 . (5分)
. (5分)(Ⅱ)由(Ⅰ)和题设知:在
 中,
中, ,
, ,
, ,
, . (6分)
. (6分) ,
,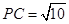 ,满足
,满足 ,
, . (7分)
. (7分)又
 ,
, ,
, 平面
平面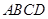 . (8分)
. (8分)过
 作
作 于
于 ,则
,则 ,
, 平面
平面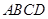 ,
, ,
, . (10分)
. (10分) . (12分)
. (12分)

练习册系列答案
相关题目
 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由. 中,截下一个棱锥
中,截下一个棱锥 ,求棱锥
,求棱锥
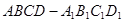 中,
中,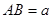 ,
,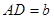 ,
,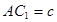 ,点
,点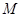 为
为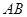 的中点,点
的中点,点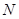 为
为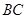 的中点.
的中点.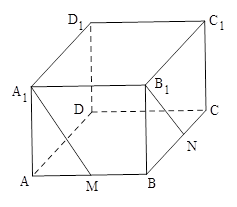
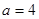 ,
,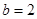 ,
,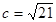 ,求异面直线
,求异面直线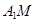 与
与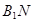 所成的角.
所成的角. 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 分别是
分别是 的中点
的中点
 ∥平面
∥平面 ;
; ;
; 的体积.
的体积.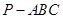 中,
中,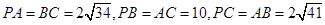 ,则三棱锥
,则三棱锥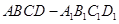 中,点
中,点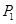 ,
,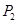 分别是线段
分别是线段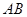 ,
,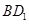 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段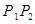 平行于平面
平行于平面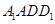 ,则四面体
,则四面体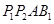 的体积的最大值是_______
的体积的最大值是_______