题目内容
19.已知函数f(x)=sinx,g(x)=2x+1.对于?x1∈[0,$\frac{7π}{6}$],都?x2∈[-m,m],使得f(x1)=g(x2).则m的取值范围是[0,$\frac{1}{4}$].分析 根据三角函数的单调性和一次函数的单调性分别求出两个函数的最值,建立关于m的不等式,解不等式即可求出m的取值范围.
解答 解:∵f(x)=sinx,
∴?x1∈[0,$\frac{7π}{6}$],
则-$\frac{1}{2}$≤sinx1≤1,
即-$\frac{1}{2}$≤f(x1)≤1,
当x2∈[-m,m]时,
g(x2)∈[-2m+1,2m+1],
若?x1∈[0,$\frac{7π}{6}$],都?x2∈[-m,m],使得f(x1)=g(x2).
则$\left\{\begin{array}{l}{2m+1≥1}\\{2m-1≤-\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥0}\\{m≤\frac{1}{4}}\end{array}\right.$,
解得0≤m≤$\frac{1}{4}$,
故m的取值范围是[0,$\frac{1}{4}$]
故答案为:[0,$\frac{1}{4}$]
点评 本题主要考查函数最值的应用,求出函数的值域,根据函数值域之间的关系是解决本题的关键.

练习册系列答案
相关题目
11.命题“?x∈(1,+∞),2x>2”的否定是( )
| A. | ?x0∈(-∞,1],${2^{x_0}}$≤2 | B. | ?x0∈(1,+∞),${2^{x_0}}$≤2 | ||
| C. | ?x∈(-∞,1],2x≤2 | D. | ?x∈(1,+∞),2x<2 |
8.函数f(x)=$\left\{\begin{array}{l}-{x^2}-2x+3,x≤0\\|{2-lnx}|,x>0\end{array}$,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次标记为a,b,c,d,下列说法错误的是( )
| A. | m∈[3,4) | |
| B. | 若关于x的方程f(x)+x=m恰有三个不同的实根,则m取值唯一 | |
| C. | $a+b+c+d∈[{{e^5}+\frac{1}{e}-2,{e^6}+\frac{1}{e^2}-2}]$ | |
| D. | abcd∈[0,e4) |
9.已知全集U={1,2,3,4,5},集合A={2,3,4},B={1,4},则(∁UA)∪B为( )
| A. | {1} | B. | {1,5} | C. | {1,4} | D. | {1,4,5} |
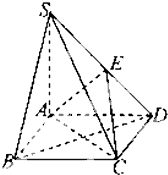 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$. 已知在三棱锥S-ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证:
已知在三棱锥S-ABC中,∠ACB=90°,又SA⊥平面ABC,AD⊥SC于D,求证: