题目内容
已知数列log2(an-1)(n∈N*)为等差数列,且a1=3,a2=5,则 =________.
=________.
1-
分析:根据题意可先求等差数列的公差d,及首项log2(a1-1),代入等差数列的通项公式可求log2(an-1),进而可求得an=2n+1,an+1-an=2n+1-2n=2n,代入等比数列的前n项和公式可求 =
=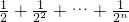 ,利用等比数列的前n项和公式可求答案.
,利用等比数列的前n项和公式可求答案.
解答:设等差数列的公差为d,则d=log2(a2-1)-log2(a1-1)=1
∴log2(an-1)=log22+(n-1)×1=n
∴an=2n+1
则an+1-an=2n+1-2n=2n
∴ =
=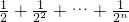 =
= =
=
故答案为:
点评:等差数列与等比数列的通项及和的求解一直是高考在数列部分的考查重点与热点之一,要求考生牢固掌握基础知识,具备一定的计算能力,才可以解决本节的问题.

分析:根据题意可先求等差数列的公差d,及首项log2(a1-1),代入等差数列的通项公式可求log2(an-1),进而可求得an=2n+1,an+1-an=2n+1-2n=2n,代入等比数列的前n项和公式可求
 =
=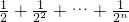 ,利用等比数列的前n项和公式可求答案.
,利用等比数列的前n项和公式可求答案.解答:设等差数列的公差为d,则d=log2(a2-1)-log2(a1-1)=1
∴log2(an-1)=log22+(n-1)×1=n
∴an=2n+1
则an+1-an=2n+1-2n=2n
∴
 =
=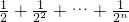 =
= =
=
故答案为:

点评:等差数列与等比数列的通项及和的求解一直是高考在数列部分的考查重点与热点之一,要求考生牢固掌握基础知识,具备一定的计算能力,才可以解决本节的问题.

练习册系列答案
相关题目