题目内容
菱形ABCD所在平面外一点P,已知PA=PC,
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)在PC上是否存在一点E,使PA∥平面EBD,证明你的结论。
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)在PC上是否存在一点E,使PA∥平面EBD,证明你的结论。
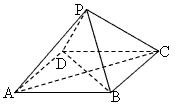
(Ⅰ)证明:∵四边形ABCD为菱形,
∴AC⊥BD,
设AC∩BD=O,
∵PA=PC,
∴AC⊥PO,
又∵BD 平面PBD,PO
平面PBD,PO 平面PBD,PO∩BD=O,
平面PBD,PO∩BD=O,
∴AC⊥平面PBD,
又AC 平面PAC,
平面PAC,
∴平面PAC⊥平面PBD;
(Ⅱ)当E为PC的中点时,PA∥平面EBD;
∵E、O分别为PC、AC的中点,
∴PA∥EO,
∵EO 平面EBD,PA
平面EBD,PA 平面EBD,
平面EBD,
∴PA∥平面EBD。

练习册系列答案
相关题目
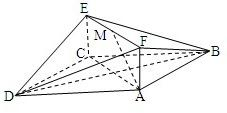 如图,菱形ABCD所在平面与矩形ACEF所在平面相互垂直,点M是线段EF的中点.
如图,菱形ABCD所在平面与矩形ACEF所在平面相互垂直,点M是线段EF的中点. 如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的所成的角是( )
如图,如果MC⊥菱形ABCD所在平面,那么MA与BD的所成的角是( ) 已知P是菱形ABCD所在平面外一点,且PB=PD,求证:平面PAC⊥平面PBD.
已知P是菱形ABCD所在平面外一点,且PB=PD,求证:平面PAC⊥平面PBD.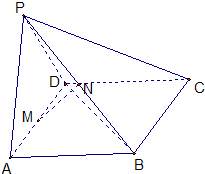 如图,P为菱形ABCD所在平面外一点,M、N 分别为AD、PB 的中点,平面PAD⊥平面ABCD,PA=PD=AD=2,∠DAB=60°求证:
如图,P为菱形ABCD所在平面外一点,M、N 分别为AD、PB 的中点,平面PAD⊥平面ABCD,PA=PD=AD=2,∠DAB=60°求证: