题目内容
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
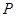 |  | 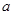 |  |  |
(Ⅱ)求
 ,
, 的值;
的值;(Ⅲ)求
 的数学期望.
的数学期望.
(Ⅰ)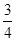 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) 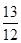 .
.
解析试题分析:(Ⅰ) 至少有一位学生做对该题,它的对立事件是一个也没做对,故可利用对立事件来求;(Ⅱ)根据 与
与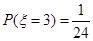 列方程求出
列方程求出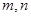 的值;(Ⅲ)由
的值;(Ⅲ)由 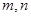 的值,可求出
的值,可求出 ,
, 的值,从而求出
的值,从而求出 的数学期望.
的数学期望.
试题解析:设“甲做对”为事件 ,“乙做对”为事件
,“乙做对”为事件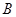 ,“丙做对”为事件
,“丙做对”为事件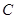 ,由题意知,
,由题意知, .
.
(Ⅰ)由于事件“至少有一位学生做对该题”与事件“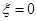 ”是对立的,所以至少有一位学生做对该题的概率是
”是对立的,所以至少有一位学生做对该题的概率是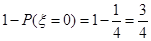 ;
;
(Ⅱ)由题意知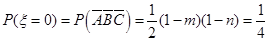 ,
,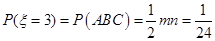 ,整理得
,整理得 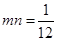 ,
, ,由
,由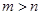 ,解得
,解得 ;
;
(Ⅲ)由题意知 ,
, 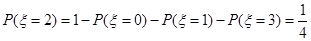 ,
,
所以 的数学期望为
的数学期望为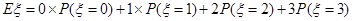
 .
.
考点:1、独立事件的概率, 2、随机变量的数学期望.

练习册系列答案
相关题目
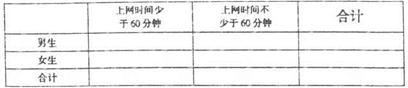
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 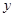 |
(1)求
 ,
,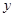 ;
;(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.

 ,
,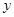 ;
; 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率. 的概率分布列及期望.
的概率分布列及期望.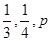 ,
, .
. 的值,
的值,




 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 四个数中任取的一个数,求
四个数中任取的一个数,求 为偶函数的概率;
为偶函数的概率; ,
, 任取的一个数,求方程
任取的一个数,求方程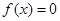 有实根的概率.
有实根的概率.