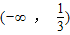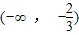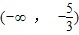题目内容
设关于x,y的不等式组
表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
|
(
,+∞)
| 2 |
| 3 |
(
,+∞)
.| 2 |
| 3 |
分析:作出不等式组对应的平面区域,要使平面区域内存在点点P(x0,y0)满足x0-2y0=2,则平面区域内必存在一个点在直线x-2y=2的下方,由图象可得m的取值范围.
解答:解:作出不等式组对应的平面如图:交点C的坐标为(m,-m),
直线x-2y=2的斜率为
, 斜截式方程为y=
斜截式方程为y=
x-1,
要使平面区域内存在点P(x0,y0)满足x0-2y0=2,
则点C(m,-m)必在直线x-2y=2的下方,
即-m<
m-1,解得m>
.
故m的取值范围是:(
,+∞).
故答案为:(
,+∞).
直线x-2y=2的斜率为
| 1 |
| 2 |
 斜截式方程为y=
斜截式方程为y=| 1 |
| 2 |
要使平面区域内存在点P(x0,y0)满足x0-2y0=2,
则点C(m,-m)必在直线x-2y=2的下方,
即-m<
| 1 |
| 2 |
| 2 |
| 3 |
故m的取值范围是:(
| 2 |
| 3 |
故答案为:(
| 2 |
| 3 |
点评:本题主要考查线性规划的基本应用,利用数形结合是解决本题的关键,综合性较强.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
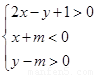 表示的平面区域内存在点P(x0,y0),满足x0-2y0=2,则m的取值范围是 ( )
表示的平面区域内存在点P(x0,y0),满足x0-2y0=2,则m的取值范围是 ( )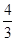 )
B.(-∞,
)
B.(-∞,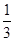 )
C.(-∞,-
)
C.(-∞,- ) D.(-∞,-
) D.(-∞,-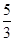 )
)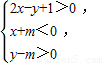 表示的平面区域内存在点P(x,y),满足x-2y=2,求得m的取值范围是( )
表示的平面区域内存在点P(x,y),满足x-2y=2,求得m的取值范围是( )