题目内容
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.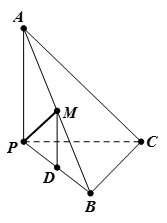
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
(1)详见解析;(2)详见解析.
解析试题分析:(1)要证明直线和平面平行,只需在平面内找一条 直线与之平行,由已知得 是
是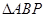 的中位线,所以
的中位线,所以 ,进而证明
,进而证明 平面
平面 ;(2)要证明面面垂直,只需在一个平面内找到另一个平面的一条垂线即可,由等边三角形
;(2)要证明面面垂直,只需在一个平面内找到另一个平面的一条垂线即可,由等边三角形 及
及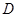 为
为 的中点,则
的中点,则 ,进而说明
,进而说明 ,进而说明
,进而说明 平面
平面 ,则有
,则有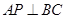 ,又由已知
,又由已知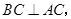 可证
可证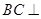 平面
平面 ,进而证明结论.
,进而证明结论.
试题解析:(1)由已知,得 是
是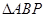 的中位线,所以
的中位线,所以 ,又
,又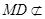 平面
平面 ,
, 平面
平面 ,故
,故 平面
平面 .
.
(2)因为 为正三角形,
为正三角形,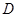 为
为 的中点,所以
的中点,所以 .所以
.所以 .又
.又

所以 平面
平面 .因为
.因为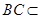 平面
平面 ,所以
,所以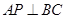 .又
.又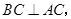
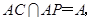 所以
所以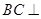 平面
平面 .因为
.因为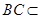 平面
平面 ,所以平面
,所以平面 ⊥平面
⊥平面 .
.
考点:1、直线和平面平行的判定;2、直线和平面垂直的判定和性质;3、面面垂直的判定.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目

 的底面是边长为
的底面是边长为 的正三角形,侧棱垂直于底面,侧棱长为
的正三角形,侧棱垂直于底面,侧棱长为 ,D为棱
,D为棱 的中点。
的中点。
 平面
平面 ;
; 的大小.
的大小.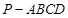 中,底面
中,底面 是菱形,
是菱形,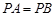 ,且侧面
,且侧面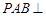 平面
平面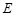 是棱
是棱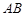 的中点.
的中点.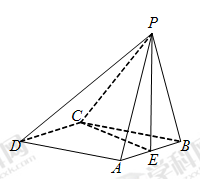
 平面
平面 ;
;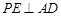 ;
;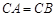 ,求证:平面
,求证:平面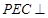 平面
平面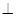 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,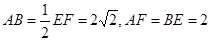 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.
 中,
中,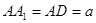 ,
,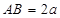 ,
,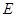 、
、  分别为
分别为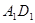 、
、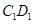 的中点.
的中点.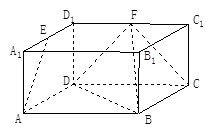
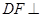 平面
平面 ;
;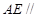 平面
平面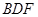 .
.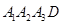 ,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.
,A1D∥A2A3,A1A2⊥A2A3,A1D=10,A1A2=8,沿△BCD三边将△A1BD、△A2BC、△A3CD翻折上去,恰好形成一个三棱锥ABCD,如图②.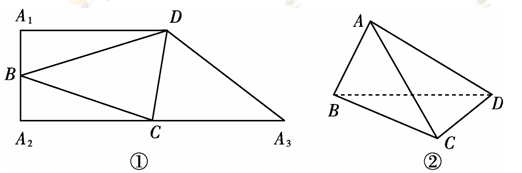
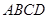 的体积。
的体积。 是一个斜三棱柱,已知
是一个斜三棱柱,已知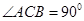 、平面
、平面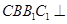 平面
平面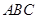 、
、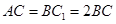 、
、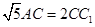 ,又
,又 、
、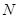 分别是
分别是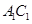 、
、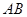 的中点.
的中点.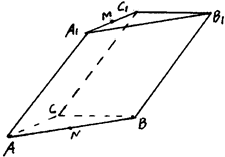
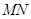 ∥平面
∥平面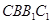 ; (2)求二面角
; (2)求二面角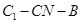 的大小.
的大小.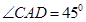 .
.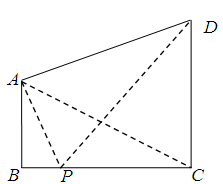
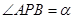 ,
, ,问点P在何处时,
,问点P在何处时,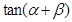 最小?
最小?