题目内容
如图,三棱柱 的底面是边长为
的底面是边长为 的正三角形,侧棱垂直于底面,侧棱长为
的正三角形,侧棱垂直于底面,侧棱长为 ,D为棱
,D为棱 的中点。
的中点。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角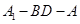 的大小.
的大小.
(Ⅰ)参考解析;(Ⅱ)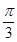
解析试题分析:(Ⅰ)要证明 平面
平面 ,主要是通过线面平行的判断定理,在平面内找一条直线与已知直线平行,通过三角形的中位线即可得到;
,主要是通过线面平行的判断定理,在平面内找一条直线与已知直线平行,通过三角形的中位线即可得到;
(Ⅱ)依题意底面是正三角形且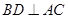 ,又可证明
,又可证明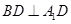 .即可得到所求的二面角
.即可得到所求的二面角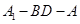 的平面角为
的平面角为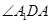 ,从而通过解直角三角形即可得到二面角的大小.本题关键是通过了解线面的关系找出二面角的平面角.
,从而通过解直角三角形即可得到二面角的大小.本题关键是通过了解线面的关系找出二面角的平面角.
试题解析:(Ⅰ)连接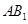 交
交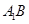 于点O,连接OD,则OD为
于点O,连接OD,则OD为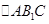 中
中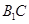 边上的中位线,所以
边上的中位线,所以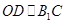 .又
.又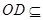 平面ABD,
平面ABD,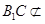 平面ABD,所以
平面ABD,所以 平面ABD.
平面ABD.
(Ⅱ)因为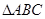 为等边三角形,D为AC中点,所以
为等边三角形,D为AC中点,所以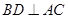 ,由侧棱垂直于底面知,三棱柱为直三棱柱,所以平面
,由侧棱垂直于底面知,三棱柱为直三棱柱,所以平面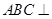 平面
平面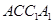 .又平面ABC
.又平面ABC 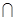 平面
平面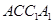 =AC,BD
=AC,BD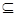 平面ABC,所以BD
平面ABC,所以BD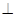 平面
平面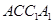 ,又AD
,又AD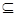 平面
平面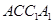 ,
,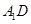
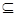 平面
平面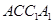 ,所以AD
,所以AD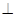 BD,
BD, 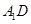
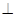 BD,故
BD,故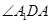 为二面角
为二面角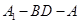 的平面角,由AC=2,
的平面角,由AC=2,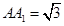 知在
知在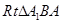 中,
中,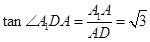 .所以
.所以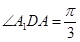 .故所求二面角的大小为
.故所求二面角的大小为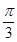 .
.
考点:1.线面平行的判定.2.面面关系.3.二面角的大小.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 是边长为2的正三角形,若
是边长为2的正三角形,若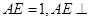 平面
平面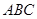 ,平面
,平面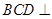 平面
平面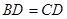 ,且
,且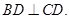
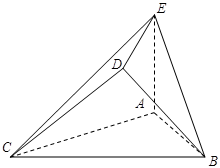
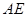 //平面
//平面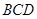 ;
;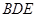
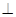 平面
平面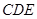 。
。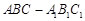 中,
中,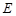 ,
,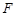 分别为
分别为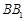 ,
, 的中点.
的中点.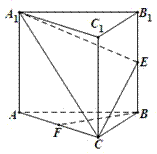
 平面
平面 ;
;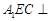 平面
平面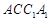 .
.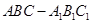 中,平面
中,平面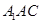 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。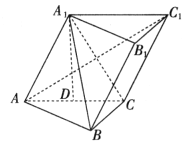
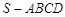 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面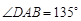 ,
, ,
,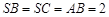 ,
,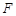 为线段
为线段 的中点.
的中点.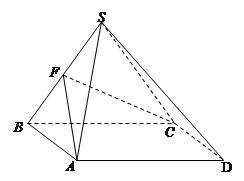
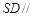 平面
平面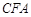 ;
;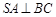 .
.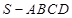 的底面是正方形,
的底面是正方形,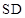 ⊥平面
⊥平面 ,
,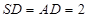
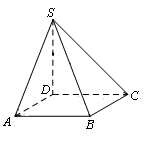
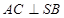 ;
;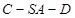 的大小.
的大小.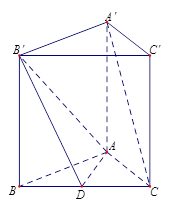
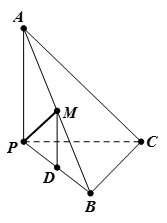
 中,已知平面
中,已知平面 ,且
,且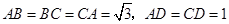 .
.
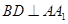 ;
;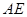 ∥平面
∥平面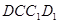 ,求
,求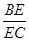 的值.
的值.