题目内容
已知椭圆的两个焦点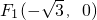 ,
,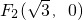 ,过F1且与坐标轴不平行的直线l1与椭圆相交于M,N两点,△MNF2的周长等于8.若过点(1,0)的直线l与椭圆交于不同两点P、Q,x轴上存在定点E(m,0),使
,过F1且与坐标轴不平行的直线l1与椭圆相交于M,N两点,△MNF2的周长等于8.若过点(1,0)的直线l与椭圆交于不同两点P、Q,x轴上存在定点E(m,0),使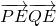 恒为定值,则E的坐标为
恒为定值,则E的坐标为
- A.

- B.

- C.

- D.

C
分析:先确定椭圆的方程,再取两个特殊位置,求出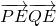 ,利用x轴上存在定点E(m,0),使
,利用x轴上存在定点E(m,0),使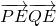 恒为定值,即可求得E的坐标.
恒为定值,即可求得E的坐标.
解答:由题意,设椭圆的方程为 (a>b>0),则c=
(a>b>0),则c= ,4a=8
,4a=8
∴a=2,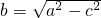 =1
=1
∴椭圆的方程为
取直线l⊥x轴,则可得P(1, ),Q(1,-
),Q(1,- ),所以
),所以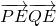 =(m-1,-
=(m-1,- )(m-1,
)(m-1, )=(m-1)2-
)=(m-1)2-
取直线l为x轴,则可得P(-2,0),Q(2,0),所以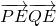 =(m+2,0)•(m-2,0)=m2-4
=(m+2,0)•(m-2,0)=m2-4
由题意可得,(m-1)2- =m2-4,∴m=
=m2-4,∴m=
∴E的坐标为
故选C.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查学生的计算能力,属于中档题.
分析:先确定椭圆的方程,再取两个特殊位置,求出
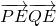 ,利用x轴上存在定点E(m,0),使
,利用x轴上存在定点E(m,0),使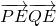 恒为定值,即可求得E的坐标.
恒为定值,即可求得E的坐标.解答:由题意,设椭圆的方程为
 (a>b>0),则c=
(a>b>0),则c= ,4a=8
,4a=8∴a=2,
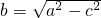 =1
=1∴椭圆的方程为

取直线l⊥x轴,则可得P(1,
 ),Q(1,-
),Q(1,- ),所以
),所以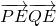 =(m-1,-
=(m-1,- )(m-1,
)(m-1, )=(m-1)2-
)=(m-1)2-
取直线l为x轴,则可得P(-2,0),Q(2,0),所以
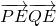 =(m+2,0)•(m-2,0)=m2-4
=(m+2,0)•(m-2,0)=m2-4由题意可得,(m-1)2-
 =m2-4,∴m=
=m2-4,∴m=
∴E的坐标为

故选C.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目