题目内容

两直角边之和为4的直角三角形面积最大值等于________．

2
分析：本题考查二次函数最大（小）值的求法．设一条直角边为x，则另一条为（4-x），则根据三角形面积公式即可得到面积S和x之间的解析式，求最值即可．
解答：设一条直角边为x，则另一条为（4-x），
∴S= $\text{[math]}$ x（4-x）=- $\text{[math]}$ （x-2）²+2，（x＞0）
∵对称轴x=2
∴即当x=2时，S_最大= $\text{[math]}$ ×2×2=2cm²．
故答案为2．
点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y=-x²-2x+5，y=3x²-6x+1等用配方法求解比较简单．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

如图所示是函数 $数学公式$ 的图象，则该函数的解析式是________．

设函数f（x）=sin（2x+ $数学公式$ ）+cos²x+ $数学公式$ sinx•cosx．
（1）求函数f（x）的最大值和最小正周期．
（2）设A，B，C为△ABC的三个内角，若cosB= $数学公式$ ，f（ $数学公式$ ）= $数学公式$ ，求sinA．

5个人分4张同样的足球票，每人至多分1张，而且票必须分完，那么不同分法的种数是

A.
5⁴
B.
4⁵
C.
5×4×3×2
D.
5

函数 $数学公式$ ，若f（-3）=5，f（3）=________．

函数 $数学公式$ 是定义在（-1，1）上的奇函数，且 $数学公式$
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）判断并证明f（x）在（-1，1）的单调性；
（Ⅲ）求满足f（t-1）+f（t）＜0的t的范围．

解不等式x²-3x-10＞0．

如图所示的曲线方程是

A.
|x|-y=0
B.
x-|y|=0
C.
$数学公式$
D.
$数学公式$

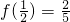
满足A=45°，c= $数学公式$ ，a=2的△ABC的个数记为m，则a^m的值为________