题目内容
定义在[-4,4]上的偶函数f(x)在区间[0,4]上单调递减,若f(1-m)<f(m),则实数m的取值范围是 .
【答案】分析:根据函数是偶函数,可得f(x)=f(|x|),利用定义在[-4,4]上的偶函数f(x)在区间[0,4]上单调递减,f(1-m)<f(m),建立不等式组,可求实数m的取值范围.
解答:解:由题意,函数是偶函数,∴f(x)=f(|x|)
∵定义在[-4,4]上的偶函数f(x)在区间[0,4]上单调递减,f(1-m)<f(m),
∴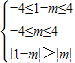
∴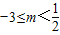
∴实数m的取值范围是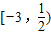
故答案为: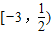
点评:本题考查函数单调性与奇偶性的结合,考查学生分析转化问题的能力,正确建立不等式组是关键.
解答:解:由题意,函数是偶函数,∴f(x)=f(|x|)
∵定义在[-4,4]上的偶函数f(x)在区间[0,4]上单调递减,f(1-m)<f(m),
∴
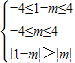
∴
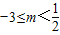
∴实数m的取值范围是
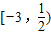
故答案为:
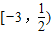
点评:本题考查函数单调性与奇偶性的结合,考查学生分析转化问题的能力,正确建立不等式组是关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
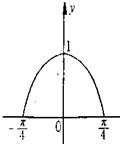 已知函y=f(x)定义在[-
已知函y=f(x)定义在[-| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=-sinx•cosx |
| C、y=sinx•cosx |
| D、y=cosx |