题目内容
若曲线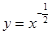 在点
在点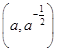 处的切线与两个坐标围成的三角形的面积为18,则
处的切线与两个坐标围成的三角形的面积为18,则 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
A
解析试题分析:因为,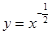 ,所以
,所以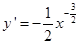 ,切线的斜率为k=-
,切线的斜率为k=-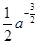 ,
,
切线方程是y-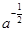 =-
=-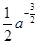 (x-a),
(x-a),
令x=0,y=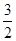
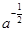 ,令y=0,x=3a,
,令y=0,x=3a,
∴三角形的面积是s=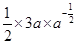 =18,解得a=64.
=18,解得a=64.
故选A.
考点:求导法则、导数的几何意义、直线方程和三角形的面积公式。
点评:小综合题,本题综合性较强,但思路比较明确,取得切线方程是关键。

练习册系列答案
相关题目
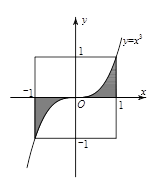
从如图所示的正方形OABC区域内任取一个点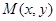 ,则点M取自阴影部分的概率为( )
,则点M取自阴影部分的概率为( )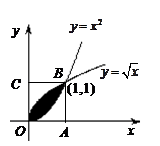
A.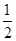 | B.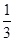 | C.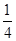 | D.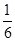 |
定义在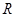 上的函数
上的函数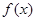 满足
满足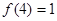 ,
,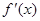 为
为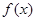 的导函数,已知
的导函数,已知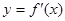 的图像如图所示,若两个正数
的图像如图所示,若两个正数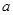 、
、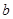 满足
满足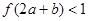 ,则
,则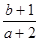 的取值范围是 ( )
的取值范围是 ( ) 
A.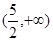 | B. | C.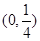 | D.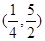 |
曲线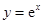 在点
在点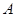 处的切线与直线
处的切线与直线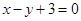 平行,则点
平行,则点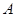 的坐标为( )
的坐标为( )
A.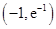 | B.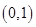 | C.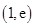 | D.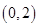 |
函数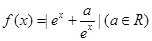 在区间
在区间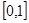 上单调递增,则
上单调递增,则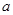 的取值范围是( )
的取值范围是( )
A.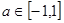 | B.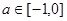 | C.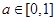 | D.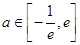 |
曲线y=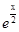 在点(4,
在点(4,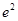 )处的切线与坐标轴所围成的三角形的面积为
)处的切线与坐标轴所围成的三角形的面积为
A.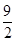 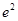 | B.4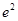 | C.2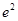 | D.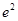 |
曲线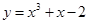 在点
在点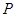 处的切线平行于直线
处的切线平行于直线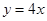 ,则点
,则点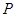 坐标是( )
坐标是( )
A. | B.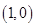 | C.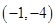 或 或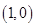 | D.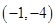 |
已知函数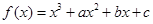 有两个极值点
有两个极值点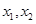 ,若
,若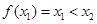 ,则关于
,则关于 的方程
的方程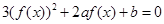 的不同实根个数为
的不同实根个数为
| A.3 | B. 4 |
| C.5 | D. 6 |
 是图中边长为2的正方形区域,
是图中边长为2的正方形区域,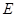 是函数
是函数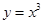 的图象与
的图象与 轴及
轴及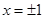 围成的阴影区域.向
围成的阴影区域.向