题目内容
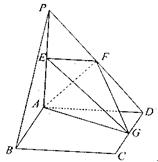
如图所示,PD⊥平面ABCD,且四边形ABCD为正方形,AB=2,E是PB的中点,
cos〈![]() ,
,![]() 〉=
〉=![]() .
.
(1)建立适当的空间坐标系,写出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
(1) 点E的坐标是(1,1,1)(2) F是AD的中点时满足EF⊥平面PCB
解析:
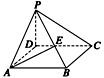
 (1)如图所示,以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
(1)如图所示,以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
则A(2,0,0)、B(2,2,0)、C(0,2,0),
设P(0,0,2m),则E(1,1,m),
∴![]() =(-1,1,m),
=(-1,1,m),
![]() =(0,0,2m).
=(0,0,2m).
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() .
.
解得m=1,∴点E的坐标是(1,1,1).
(2)∵F∈平面PAD,∴可设F(x,0,z).
则![]() =(x-1,-1,z-1),
=(x-1,-1,z-1),
又![]() =(2,0,0),
=(2,0,0),![]() =(0,2,-2)
=(0,2,-2)
∵EF⊥平面PCB
∴![]() ⊥
⊥![]() ,且
,且![]() ⊥
⊥![]()
即![]()
∴![]()
∴![]() ,∴F点的坐标为(1,0,0)
,∴F点的坐标为(1,0,0)
即点F是AD的中点时满足EF⊥平面PCB.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
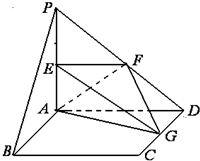 如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点.
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点. 如图所示的平面直角坐标系xoy中,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若
如图所示的平面直角坐标系xoy中,已知直线l与半径为1的⊙D相切于点C,动点P到直线l的距离为d,若