题目内容
当x∈(3,4)时,不等式 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是
- A.
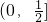
- B.
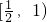
- C.(1,2]
- D.[2,+∞)
B
分析:由题意可得, 在(3,4)上恒成立,从而只要,
在(3,4)上恒成立,从而只要, 在(3,4)上的最小值即可
在(3,4)上的最小值即可
解答:由题意可得, 在(3,4)上恒成立
在(3,4)上恒成立
令f(x)=loga(x-2),g(x)=-(x-3)2
则f(x)<g(x)min
∵3<x<4时,g(x)=-(x-3)2单调递减
∴g(x)∈(-1,0)
∴loga(x-2)≤-1在x∈(3,4)恒成立
∵3<x<4
∴1<x-2<2
当a>1时,0<loga(x-2)不满足题意
∴0<a<1
∴y=loga(x-2)在(3,4)上单调递减
若使不等式, 在(3,4)上恒成立
在(3,4)上恒成立
∴loga2≤-1
∴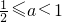
故选B
点评:本题主要考查了利用函数的恒成立求解参数的范围,解题的关键是求出相应函数的最值.体现了转化思想在求解中的应用.
分析:由题意可得,
 在(3,4)上恒成立,从而只要,
在(3,4)上恒成立,从而只要, 在(3,4)上的最小值即可
在(3,4)上的最小值即可解答:由题意可得,
 在(3,4)上恒成立
在(3,4)上恒成立令f(x)=loga(x-2),g(x)=-(x-3)2
则f(x)<g(x)min
∵3<x<4时,g(x)=-(x-3)2单调递减
∴g(x)∈(-1,0)
∴loga(x-2)≤-1在x∈(3,4)恒成立
∵3<x<4
∴1<x-2<2
当a>1时,0<loga(x-2)不满足题意
∴0<a<1
∴y=loga(x-2)在(3,4)上单调递减
若使不等式,
 在(3,4)上恒成立
在(3,4)上恒成立∴loga2≤-1
∴
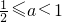
故选B
点评:本题主要考查了利用函数的恒成立求解参数的范围,解题的关键是求出相应函数的最值.体现了转化思想在求解中的应用.

练习册系列答案
相关题目