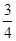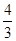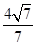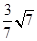题目内容
如图,椭圆 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.

(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.(I)  (II)
(II)  和0时,
和0时, 取得最大值
取得最大值
 (II)
(II)  和0时,
和0时, 取得最大值
取得最大值
(I) ……①
……①
矩形ABCD面积为8,即 ……②
……②
由①②解得: ,∴椭圆M的标准方程是
,∴椭圆M的标准方程是 .
.
(II) ,
,
设 ,则
,则 ,
,
由 得
得 .
.
 .
.
当 过
过 点时,
点时, ,当
,当 过
过 点时,
点时, .
.
①当 时,有
时,有 ,
,
 ,
,
其中 ,由此知当
,由此知当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.
②由对称性,可知若 ,则当
,则当 时,
时, 取得最大值
取得最大值 .
.
③当 时,
时, ,
, ,
,
由此知,当 时,
时, 取得最大值
取得最大值 .
.
综上可知,当 和0时,
和0时, 取得最大值
取得最大值
 ……①
……①矩形ABCD面积为8,即
 ……②
……②由①②解得:
 ,∴椭圆M的标准方程是
,∴椭圆M的标准方程是 .
.(II)
 ,
,设
 ,则
,则 ,
,由
 得
得 .
. .
.当
 过
过 点时,
点时, ,当
,当 过
过 点时,
点时, .
.①当
 时,有
时,有 ,
, ,
,其中
 ,由此知当
,由此知当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.②由对称性,可知若
 ,则当
,则当 时,
时, 取得最大值
取得最大值 .
.③当
 时,
时, ,
, ,
,由此知,当
 时,
时, 取得最大值
取得最大值 .
.综上可知,当
 和0时,
和0时, 取得最大值
取得最大值

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
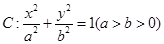 的焦点和上顶点分别为
的焦点和上顶点分别为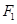 、
、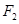 、
、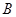 ,我们称
,我们称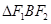 为椭圆
为椭圆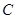 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断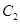 与
与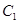 是否相似,如果相似则求出
是否相似,如果相似则求出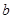 的椭圆为
的椭圆为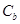 ,且直线
,且直线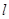 与椭圆为
与椭圆为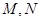 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,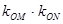 是否与
是否与
 是椭圆
是椭圆 上的一点,若
上的一点,若 ,则点
,则点 ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程
的方程 的离心率为
的离心率为 ,长轴长为
,长轴长为 ,直线
,直线 交椭圆于不同的两点A、B.
交椭圆于不同的两点A、B. 的值(O点为坐标原点);
的值(O点为坐标原点);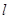 的距离为
的距离为 ,求
,求 面积的最大值.
面积的最大值.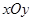 中,椭圆
中,椭圆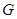 的中心为坐标原点,左焦点为
的中心为坐标原点,左焦点为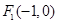 ,
, 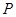 为椭圆
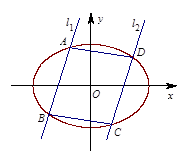
为椭圆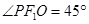 .
.
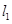 :
: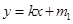 与椭圆
与椭圆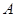 ,
,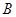 两点,直线
两点,直线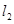 :
: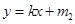 (
(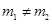 )与椭圆
)与椭圆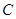 ,
,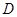 两点,且
两点,且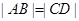 ,如图所示.
,如图所示.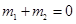 ;
;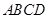 的面积
的面积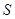 的最大值.
的最大值.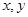 的方程
的方程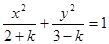 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则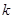 的取值范围为
的取值范围为 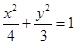 上的一点,
上的一点,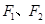 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若 的内切圆的半径为
的内切圆的半径为 ,则
,则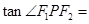 ( )
( )