题目内容
数列{bn}的首项b1=1,前n项和为Sn,点(n,Sn)、(4,10)都在二次函数y=ax2+bx的图象上,数列{an}满足
=2n.
(Ⅰ)求证:数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=(1-
)
,Rn=
+
+
+…+
.试比较Rn与
的大小,并证明你的结论.
| bn |
| an |
(Ⅰ)求证:数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=(1-
| 1 |
| n+1 |
| 1 |
| an |
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 5n |
| 2n+1 |
(Ⅰ)证明:∵b1=1,∴S1=1
∴点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上
∴a+b=1,16a+4b=10,解得a=
,b=
.
∴Sn=
n2+
n.则n≥2时,Sn-1=
(n-1)2+
(n-1).
∴bn=Sn-Sn-1=
n2+
n-[
(n-1)2+
(n-1)]=n(n≥2).
又b1=1也适合,所以bn=n(n∈N+).则bn-bn-1=1.
∴数列{bn}是首项为1,公差为1的等差数列.
又
=2n ∴an=
=
.
(Ⅱ)证明:∵cn=(1-
)
=
•
=
∴
=
∴Rn=
+
+
+…+
=
+
+
+…+
①.
∴
Rn=
+
+
+…+
,②
两式相减得
Rn=
+
+
+…+
-
∴Rn=3-
,Rn-
=
.
所以只需要比较2n与2n+1的大小即可.
当n=1时,2n<2n+1,所以Rn<
,
当n=2时,2n<2n+1,所以Rn<
,
当n≥3时,2n=(1+1)n=1+n++n+1>2n+1,所以Rn>
.(12分)
∴点(1,1)、(4,10)都在二次函数y=ax2+bx的图象上
∴a+b=1,16a+4b=10,解得a=
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又b1=1也适合,所以bn=n(n∈N+).则bn-bn-1=1.
∴数列{bn}是首项为1,公差为1的等差数列.
又
| bn |
| an |
| bn |
| 2n |
| n |
| 2n |
(Ⅱ)证明:∵cn=(1-
| 1 |
| n+1 |
| 1 |
| an |
| n |
| n+1 |
| 2n |
| n |
| 2n |
| n+1 |
| 1 |
| cn |
| n+1 |
| 2n |
∴Rn=
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| c3 |
| 1 |
| cn |
| 1+1 |
| 2 |
| 2+1 |
| 22 |
| 3+1 |
| 23 |
| n+1 |
| 2n |
∴
| 1 |
| 2 |
| 1+1 |
| 22 |
| 2+1 |
| 23 |
| 3+1 |
| 24 |
| n+1 |
| 2n+1 |
两式相减得
| 1 |
| 2 |
| 1+1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n+1 |
| 2n+1 |
∴Rn=3-
| 3+n |
| 2n |
| 5n |
| 2n+1 |
| (n+3)(2n-2n-1) |
| 2n(2n+1) |
所以只需要比较2n与2n+1的大小即可.
当n=1时,2n<2n+1,所以Rn<
| 5n |
| 2n+1 |
当n=2时,2n<2n+1,所以Rn<
| 5n |
| 2n+1 |
当n≥3时,2n=(1+1)n=1+n++n+1>2n+1,所以Rn>
| 5n |
| 2n+1 |

练习册系列答案
相关题目
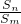 =
=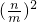 .
.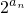 +bn+11≥0成立,求实数b的最小值.
+bn+11≥0成立,求实数b的最小值.