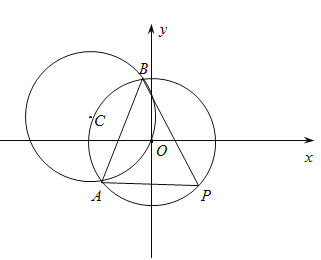
题目内容
【题目】已知抛物线C:![]() ,其焦点到准线的距离为2,直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的切线
,其焦点到准线的距离为2,直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的切线![]() ,
,![]() 交于点M
交于点M
(Ⅰ)求抛物线C的方程
(Ⅱ)若![]() ,求三角形
,求三角形![]() 面积的最小值
面积的最小值
【答案】(Ⅰ)![]() ;
;
(Ⅱ)4.
【解析】
(Ⅰ)焦点到准线的距离为2,等价于![]() ,即可得出答案。
,即可得出答案。
(Ⅱ)设出![]() ,
,![]() 两点,分别写出其切线
两点,分别写出其切线![]() ,
,![]() 与点
与点![]() ,由
,由![]() 可得到
可得到![]() ,
,
再设出直线l的方程,联立直线与直线l,由![]() 可得直线l为
可得直线l为![]() ,最后求出
,最后求出![]() 到直线l的距离,与
到直线l的距离,与![]() ,即可用
,即可用![]() 表示出
表示出![]() 的面积,即可求出其最小值。
的面积,即可求出其最小值。
(Ⅰ)焦点到准线的距离为2,即![]() ,所以求抛物线C的方程为
,所以求抛物线C的方程为![]()
(Ⅱ)抛物线的方程为![]() ,即
,即![]() ,所以
,所以![]()
设![]() ,
,![]() ,
,
![]() :
:![]() ,
,![]() :
:![]()
由于![]() ,所以
,所以![]() ,即
,即![]()
设直线l方程为![]() ,与抛物线方程联立,得
,与抛物线方程联立,得![]() 所以
所以![]()
![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即l:
,即l:![]()
联立方程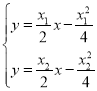 得
得![]() ,即:
,即:![]()
M点到直线l的距离
![]()
所以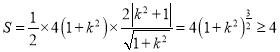
当![]() 时,
时,![]() 面积取得最小值4.
面积取得最小值4.

练习册系列答案
相关题目