题目内容
设函数 (其中
(其中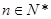 ),区间
),区间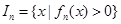 .
.
(Ⅰ)定义区间 的长度为
的长度为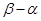 ,求区间
,求区间 的长度;
的长度;
(Ⅱ)把区间 的长度记作数列
的长度记作数列 ,令
,令 ,
,
(1)求数列 的前
的前 项和
项和 ;
;
(2)是否存在正整数 ,
, (
(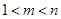 ),使得
),使得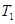 ,
,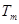 ,
, 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)
;(2)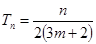 ;
;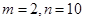 .
.
解析试题分析:(1)掌握一元二次不等式的解法;(2)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的;(3)与数列有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
试题解析:解:(Ⅰ)由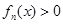 ,得
,得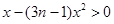 ,解得
,解得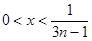 ,
,
即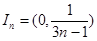 ,所以区间
,所以区间 的长度为
的长度为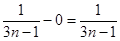 ; 3分
; 3分
(Ⅱ)由(Ⅰ)知 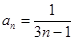 .
.
(1)∵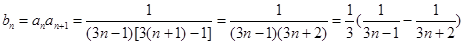
∴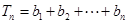
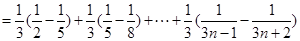
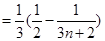
 6分
6分
(2)由(1)知,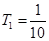 ,
,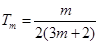 ,
,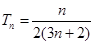
假设存在正整数 、
、
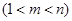 ,使得
,使得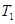 、
、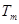 、
、 成等比数列,则
成等比数列,则  ,
,
即 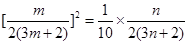 , 经化简得
, 经化简得 .
.
∴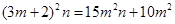 ∴
∴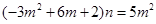 (*)
(*)
当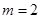 时,(*)式可化为
时,(*)式可化为 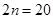 ,所以
,所以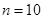 .
.
当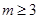 时,
时,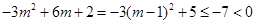 .
.
又∵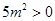 ,∴(*)式可化为
,∴(*)式可化为 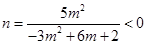 ,所以此时
,所以此时 无正整数解.
无正整数解.
综上可知,存在满足条件的正整数 、
、 ,此时
,此时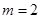 ,
,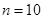 . 10分
. 10分
考点:(1)一元二次不等式的解法;(2)裂项法求和;(3)证明存在性问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
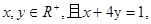 则
则 的最大值为 .
的最大值为 .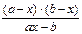 <0的解集是______.
<0的解集是______. ,不等式
,不等式 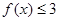 的解集是
的解集是 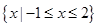
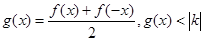 存在实数解,求实数
存在实数解,求实数  的取值范围。
的取值范围。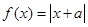 .
.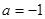 时,求不等式
时,求不等式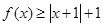 的解集;
的解集;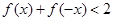 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围. ,(1)当a=2时,求关于x的不等式
,(1)当a=2时,求关于x的不等式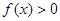 的解集;(2)当a>0时,求关于x的不等式
的解集;(2)当a>0时,求关于x的不等式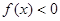 的解集.
的解集. 使不等式
使不等式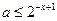 在
在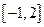 成立,则
成立,则