题目内容
已知 ,不等式
,不等式 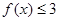 的解集是
的解集是 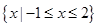
(Ⅰ)求a的值;
(Ⅱ)若 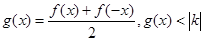 存在实数解,求实数
存在实数解,求实数  的取值范围。
的取值范围。
(Ⅰ)-2;(Ⅱ)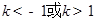
解析试题分析:(Ⅰ)由含绝对值不等式解法转化为关于 的一元一次不等式组求解,因为一次项系数含参数,故需要分类讨论解出解决与已知原不等式解集比较,列出关于
的一元一次不等式组求解,因为一次项系数含参数,故需要分类讨论解出解决与已知原不等式解集比较,列出关于 的方程,从而求出
的方程,从而求出 的值;(Ⅱ)由(Ⅰ)知
的值;(Ⅱ)由(Ⅰ)知 的值,将
的值,将 的解析式具体化,利用含绝对值不等式性质,求出
的解析式具体化,利用含绝对值不等式性质,求出 的最小值,
的最小值,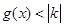 存在实数解,故
存在实数解,故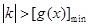 ,解此不等式得出不等式的解集就是实数
,解此不等式得出不等式的解集就是实数  的取值范围.
的取值范围.
试题解析:(Ⅰ)由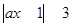 得:
得: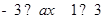 即
即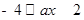
当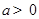 时,
时,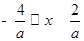
 原不等式的解集是
原不等式的解集是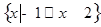
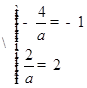 ,无解;
,无解;
当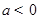 时,
时,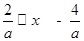
 原不等式的解集是
原不等式的解集是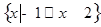
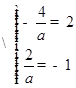 ,得
,得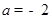 (5分)
(5分)
(Ⅱ)由题: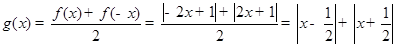
因为 存在实数解,只需
存在实数解,只需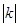 大于
大于 的最小值
的最小值
由绝对值的几何意义,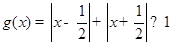 ,所以
,所以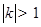
解得: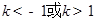 (10分)
(10分)
考点:含绝对值不等式解法,含绝对值不等式性质,分类整合思想,含参数不等式有解问题

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 上恒成立,则实数a的取值范围是 .
上恒成立,则实数a的取值范围是 .  的定义域为集合A,关于x的不等式
的定义域为集合A,关于x的不等式 的解集为B,求使
的解集为B,求使 的取值范围.
的取值范围. (其中
(其中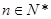 ),区间
),区间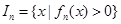 .
. 的长度为
的长度为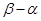 ,求区间
,求区间 的长度;
的长度; ,令
,令 ,
, 的前
的前 项和
项和 ;
; ,
,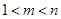 ),使得
),使得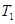 ,
,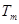 ,
,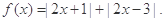
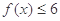 的解集;
的解集; 的不等式
的不等式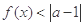 的解集非空,求实数
的解集非空,求实数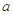 的取值范围.
的取值范围.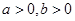 ,且
,且 ,若
,若 恒成立.
恒成立.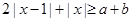 对任意的
对任意的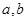 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围. 则
则 的解集为________.
的解集为________. 的解集为 (结果写成集合的形式)
的解集为 (结果写成集合的形式)