ЬтФПФкШн
ЁОЬтФПЁПЮЊЯьгІЙњМвЬсГіЕФЁАДѓжкДДвЕЃЌЭђжкДДаТЁБЕФКХей,аЁРюЭЌбЇДѓбЇБЯвЕКѓ,ОіЖЈРћгУЫљбЇзЈвЕНјаазджїДДвЕЁЃОЙ§ЪаГЁЕїВщ,ЩњВњФГаЁаЭЕчзгВњЦЗашЭЖШыФъЙЬЖЈГЩБОЮЊ5ЭђдЊЃЌУПФъЩњВњ![]() ЭђМўЃЌашСэЭЖШыСїЖЏГЩБОЮЊ
ЭђМўЃЌашСэЭЖШыСїЖЏГЩБОЮЊ![]() ЭђдЊЃЌЧв
ЭђдЊЃЌЧв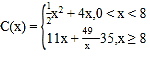 ЃЌУПМўВњЦЗЪлМлЮЊ10дЊЁЃОЪаГЁЗжЮі,ЩњВњЕФВњЦЗЕБФъФмШЋВПЪлЭъЁЃ
ЃЌУПМўВњЦЗЪлМлЮЊ10дЊЁЃОЪаГЁЗжЮі,ЩњВњЕФВњЦЗЕБФъФмШЋВПЪлЭъЁЃ
(1)аДГіФъРћШѓ![]() (ЭђдЊ)ЙигкФъВњСП
(ЭђдЊ)ЙигкФъВњСП![]() (ЭђМў)ЕФКЏЪ§НтЮіЪНЃЛ
(ЭђМў)ЕФКЏЪ§НтЮіЪНЃЛ
(зЂ:ФъРћШѓ=ФъЯњЪлЪеШы-ЙЬЖЈГЩБО-СїЖЏГЩБО)
(2)ФъВњСПЮЊЖрЩйЭђМўЪБЃЌаЁРюдкетвЛВњЦЗЕФЩњВњжаЫљЛёРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩй?
ЁОД№АИЁПЃЈ1ЃЉ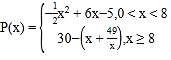 ЃЛ
ЃЛ
ЃЈ2ЃЉЕБФъВњСПЮЊ8ЭђМўЪБЃЌаЁРюдкетвЛВњЦЗЕФЩњВњжаЫљЛёРћШѓзюДѓЃЌзюДѓРћШѓЮЊ![]() ЭђдЊЁЃ
ЭђдЊЁЃ
ЁОНтЮіЁП
ЃЈ1ЃЉвђЮЊУПМўВњЦЗЪлМлЮЊ10дЃЌдђ![]() ЭђМўВњЦЗЯњЪлЪеШыЮЊ
ЭђМўВњЦЗЯњЪлЪеШыЮЊ![]() ЭђдЊЃЌЗжСНжжЧщПіЬжТлЃЌЕБ
ЭђдЊЃЌЗжСНжжЧщПіЬжТлЃЌЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБЃЌЗжБ№РћгУЯњЪлЪеШыМѕШЅГЩБОПЩЕУГіФъРћШѓ
ЪБЃЌЗжБ№РћгУЯњЪлЪеШыМѕШЅГЩБОПЩЕУГіФъРћШѓ![]() (ЭђдЊ)ЙигкФъВњСП
(ЭђдЊ)ЙигкФъВњСП![]() (ЭђМў)ЕФКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉЕБ
(ЭђМў)ЕФКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЕУ
ЪБЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЕУ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]() ЃЌгЩ
ЃЌгЩ![]() ПЩЕУНсЙћ.
ПЩЕУНсЙћ.
ЃЈ1ЃЉвђЮЊУПМўВњЦЗЪлМлЮЊ10дЊЃЌдђ![]() ЭђМўВњЦЗЯњЪлЪеШыЮЊ
ЭђМўВњЦЗЯњЪлЪеШыЮЊ![]() ЭђдЊЃЌ
ЭђдЊЃЌ
вРЬтвтЕУЃК
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ыљвд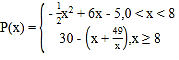
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЮЊМѕКЏЪ§ЃЌ
ЮЊМѕКЏЪ§ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]()
ЙЪЕБФъВњСПЮЊ8ЭђМўЪБЃЌаЁРюдкетвЛВњЦЗЕФЩњВњжаЫљЛёРћШѓзюДѓЃЌзюДѓРћШѓЮЊ![]() ЭђдЊ
ЭђдЊ