题目内容
已知-| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
分析:由已知的一元二次方程,利用韦达定理求出两根之和与两根之积,即可得到tanα+tanβ及tanα•tanβ的值,然后利用两角和的正切函数公式表示出tan(α+β),把tanα+tanβ及tanα•tanβ的值代入即可求出tan(α+β)的值,由α和β的范围,求出α+β的范围,利用特殊角的三角函数值即可求出α+β的度数.
解答:解:∵tanα+tanβ=-6,tanα•tanβ=7(4分)
∵tan(α+β)=
=
=1(8分)
∴tanα<0,tanβ<0
∴-
<α<0,-
<β<0(12分)
∴-π<α+β<0,
∴α+β=-
(14分)
∵tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
| -6 |
| 1-7 |
∴tanα<0,tanβ<0
∴-
| π |
| 2 |
| π |
| 2 |
∴-π<α+β<0,
∴α+β=-
| 3π |
| 4 |
点评:此题考查了两角和与差的正切函数公式,以及一元二次方程的根的分布与系数的关系.熟练掌握公式及关系是解本题的关键,同时在解题时注意角度的范围.

练习册系列答案
相关题目
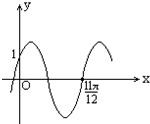
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|