题目内容
18.已知cosα=-$\frac{4}{5}$,且α∈($\frac{π}{2}$,π),则tan($\frac{π}{4}$-α)=7.分析 由已知利用同角三角函数基本关系式可求sinα,tanα的值,进而利用特殊角的三角函数值及两角差的正切函数公式即可计算求值得解.
解答 解:∵cosα=-$\frac{4}{5}$,且α∈($\frac{π}{2}$,π),
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{3}{5}$,tan$α=\frac{sinα}{cosα}$=-$\frac{3}{4}$,
∴tan($\frac{π}{4}$-α)=$\frac{1-tanα}{1+tanα}$=7.
故答案为:7.
点评 本题主要考查了同角三角函数基本关系式,特殊角的三角函数值及两角差的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
10.若θ是直线l的倾斜角,且sinθ+cosθ=$\frac{{\sqrt{5}}}{5}$,则l的斜率为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$或-2 | C. | $\frac{1}{2}$或2 | D. | -2 |
6.等差数列{an}的公差为d,an>0,前n项和为Sn,若a2,S3,a2+S5成等比数列,则$\frac{d}{a_1}$=( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
13.已知一空间几何体的三视图如图所示,其中俯视图为正方形,则该几何体的外接球的表面积为( )


| A. | 27π | B. | 49π | C. | 81π | D. | 100π |
8.已知正方体的棱长为2,则此正方体全面积是( )
| A. | 4 | B. | 12 | C. | 24 | D. | 48 |
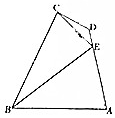 如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$
如图,在平面四边形ABCD中,DA⊥AB,CE⊥BE,DE=1,DC=2,AB=2$\sqrt{7}$,∠CDE=$\frac{2π}{3}$