题目内容
面积为 的平面凸四边形的第
的平面凸四边形的第 条边的边长记为
条边的边长记为 ,此四边形内任一点
,此四边形内任一点 到第
到第 条边的距离为
条边的距离为 ,(i)若
,(i)若 ,则
,则 ;(ii)类比以上性质,体积为
;(ii)类比以上性质,体积为 的三棱锥的第
的三棱锥的第 个面的面积记为
个面的面积记为 ,此三棱锥内任一点
,此三棱锥内任一点 到第
到第 个面的距离记为
个面的距离记为 ,若
,若 ,则
,则 .
.
 的平面凸四边形的第
的平面凸四边形的第 条边的边长记为
条边的边长记为 ,此四边形内任一点
,此四边形内任一点 到第
到第 条边的距离为
条边的距离为 ,(i)若
,(i)若 ,则
,则 ;(ii)类比以上性质,体积为
;(ii)类比以上性质,体积为 的三棱锥的第
的三棱锥的第 个面的面积记为
个面的面积记为 ,此三棱锥内任一点
,此三棱锥内任一点 到第
到第 个面的距离记为
个面的距离记为 ,若
,若 ,则
,则 .
. ;
;
分别利用分割面积与体积即可。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目

 },(n∈N
},(n∈N )是等差数列,则有数列b
)是等差数列,则有数列b (n∈N
(n∈N ,请依据:
,请依据: ;
; ;
; ;归纳出
;归纳出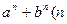 为正整数)满足的不等式,并予以证明;
为正整数)满足的不等式,并予以证明; -i为纯虚数,则实数a= 。
-i为纯虚数,则实数a= 。 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 成立时,总可推出
成立时,总可推出
 成立”。那么,下列命题总成立的是( )
成立”。那么,下列命题总成立的是( ) 成立,则
成立,则 成立
成立 成立,则
成立,则 成立
成立 成立,则当
成立,则当 时,均有
时,均有 成立
成立 成立,则当
成立,则当 时,均有
时,均有 ,计算得
,计算得 ,
, ,
, ,
, ,观察上述结果,可推测一般的结论为 .
,观察上述结果,可推测一般的结论为 . 等于 ( )
等于 ( )



 的圆的内接矩形中,以正方形的面积为最大,最大值为
的圆的内接矩形中,以正方形的面积为最大,最大值为 .”猜想关于球的相应命题为“半径为
.”猜想关于球的相应命题为“半径为 的虚部为
的虚部为


