题目内容
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(Ⅰ)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅱ)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
![]() 【解析】
【解析】
 (Ⅲ)解法1是考虑到函数
(Ⅲ)解法1是考虑到函数![]() 在
在![]() 上单调递增这个性质,利用
上单调递增这个性质,利用![]() ,利用同向不等式相加性得到
,利用同向不等式相加性得到![]()
![]() ,结合
,结合![]()
![]()

![]()
![]() ,
,
∴切线![]() 的方程为:
的方程为:![]() ,
,
又![]() 切线
切线![]() 过点
过点![]() ,
,

 ,
,
把( * )式代入,得![]() ,
,

化简,得![]() ,
,
![]() ,
,![]() . (3)
. (3)
把(*)式代入(3),解得![]() .
.
![]() 存在
存在![]() ,使得点
,使得点![]() 、
、![]() 与
与![]() 三点共线,且
三点共线,且 ![]() .
.
(Ⅲ)解法![]() :易知
:易知![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]()
![]()
![]() ,
,
则![]() .
.

![]() .
.



练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
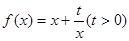 和点
和点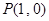 ,过点
,过点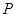 作曲线
作曲线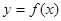 的两条切线
的两条切线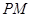 、
、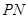 ,切点分别为
,切点分别为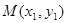 、
、 .
.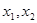 为关于
为关于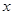 的方程
的方程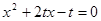 的两根;
的两根;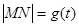 ,求函数
,求函数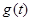 的表达式;
的表达式;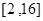 内总存在
内总存在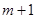 个实数
个实数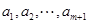 (可以相同),使得不等式
(可以相同),使得不等式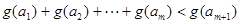 成立,求
成立,求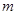 的最大值.
的最大值.