题目内容
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(Ⅰ)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅱ)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
![]()
【解析】

![]() ,结合
,结合![]()
![]()
进而得到![]() ,由于
,由于![]() ,于是得到
,于是得到![]() ,求出
,求出![]() 的取值范围,进
的取值范围,进
![]()
![]() ,
,
∴切线![]() 的方程为:
的方程为:![]() ,
,

由(1)、(2),可得![]() 是方程
是方程![]() 的两根,
的两根,
 ( * )
( * )

 ,
,

化简,得![]() ,
,



解法![]() :依题意,当区间
:依题意,当区间![]() 的长度最小时,
的长度最小时,
得到的![]() 最大值,即是所求值.
最大值,即是所求值.
![]() ,
,![]() 长度最小的区间为
长度最小的区间为![]()
当![]()
![]() 时,与解法
时,与解法![]() 相同分析,得
相同分析,得![]() ,
,


练习册系列答案
相关题目
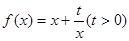 和点
和点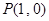 ,过点
,过点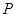 作曲线
作曲线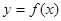 的两条切线
的两条切线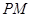 、
、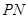 ,切点分别为
,切点分别为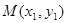 、
、 .
.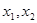 为关于
为关于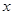 的方程
的方程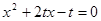 的两根;
的两根;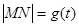 ,求函数
,求函数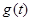 的表达式;
的表达式;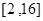 内总存在
内总存在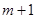 个实数
个实数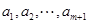 (可以相同),使得不等式
(可以相同),使得不等式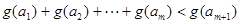 成立,求
成立,求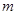 的最大值.
的最大值.