题目内容
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(1)求证:![]() 为关于
为关于![]() 的方程
的方程![]() 的两根;
的两根;
(2)设![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(3)在(2)的条件下,若在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() (可以相同),使得不等,则m的最大值,
(可以相同),使得不等,则m的最大值,![]() 为正整数
为正整数
![]() ,
,![]() 的最大值为
的最大值为![]() .
.
解析:
解: (1)由题意可知:![]()
∵ ![]() ,
,
∴切线![]() 的方程为:
的方程为:![]() ,
,
又![]() 切线
切线![]() 过点
过点![]() ,
, ![]() 有
有![]() ,
,
即![]() , ①
, ①
同理,由切线![]() 也过点
也过点![]() ,得
,得![]() .②
.②
由①、②,可得![]() 是方程
是方程![]() ( * )的两根
( * )的两根
(2)由( * )知. 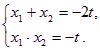
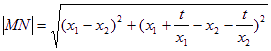
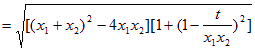
![]() ,
,
∴ ![]() .
.
(3)易知![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]()
![]()
![]() ,
,
则![]() .
.
即![]() ,即
,即![]() ,
,
所以![]() ,由于
,由于![]() 为正整数,所以
为正整数,所以![]() .
.
又当![]() 时,存在
时,存在![]() ,
,![]() 满足条件,
满足条件,
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
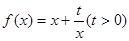 和点
和点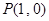 ,过点
,过点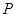 作曲线
作曲线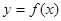 的两条切线
的两条切线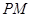 、
、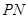 ,切点分别为
,切点分别为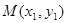 、
、 .
.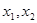 为关于
为关于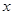 的方程
的方程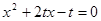 的两根;
的两根;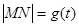 ,求函数
,求函数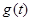 的表达式;
的表达式;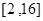 内总存在
内总存在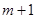 个实数
个实数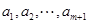 (可以相同),使得不等式
(可以相同),使得不等式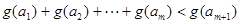 成立,求
成立,求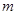 的最大值.
的最大值.