题目内容
如图,FD垂直于矩形ABCD所在平面,CE//DF, .
.

(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB = ,EF =
,EF =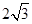 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
 .
.
(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB =
 ,EF =
,EF =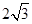 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?(Ⅰ)见解析
(Ⅱ)
(Ⅱ)

解(Ⅰ)法1:过点E作CD的平行线交DF于点M,连接AM.
因为CE//DF,所以四边形CEMD是平行四边形.可得EM = CD且EM //CD,于是四边形BEMA也是平行四边形,所以有BE//AM,而直线BE在平面ADF外,所以BE//平面ADF. 6分

法2:以直线DA为x轴,直线DC为y轴,直线DF为z轴,建立空间直角坐标系.则平面ADF的一个法向量为 .
.
设AB = a,BC = b,CE = c,则点B、E的坐标分别为(b,a,0)和(0,a,c),那么向量 .可知
.可知 ,得
,得 ,而直线BE在平面ADF的外面,所以BE//平面ADF.
,而直线BE在平面ADF的外面,所以BE//平面ADF.
(Ⅱ)由EF =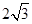 ,EM =" AB" =
,EM =" AB" = ,得FM = 3且
,得FM = 3且 .
.
由 可得FD = 4,从而得CE =1. 8分
可得FD = 4,从而得CE =1. 8分
设BC = a,则点B的坐标为(a, ,0).又点E、F的坐标分别为(0,
,0).又点E、F的坐标分别为(0, ,1)和(0,0,4),所以
,1)和(0,0,4),所以 ,
, .
.
设平面BEF的一个法向量为 ,则
,则 ,解得一组解为
,解得一组解为 ,所以
,所以 . 10分
. 10分
易知平面DEF的一个法向量为 ,可得
,可得

由于此时 就是二面角B-EF-D的大小,所以
就是二面角B-EF-D的大小,所以 ,可得
,可得 .
.
所以另一边BC的长为 时,二面角B-EF-D的大小为45°. 12分
时,二面角B-EF-D的大小为45°. 12分
因为CE//DF,所以四边形CEMD是平行四边形.可得EM = CD且EM //CD,于是四边形BEMA也是平行四边形,所以有BE//AM,而直线BE在平面ADF外,所以BE//平面ADF. 6分

法2:以直线DA为x轴,直线DC为y轴,直线DF为z轴,建立空间直角坐标系.则平面ADF的一个法向量为
 .
.设AB = a,BC = b,CE = c,则点B、E的坐标分别为(b,a,0)和(0,a,c),那么向量
 .可知
.可知 ,得
,得 ,而直线BE在平面ADF的外面,所以BE//平面ADF.
,而直线BE在平面ADF的外面,所以BE//平面ADF.(Ⅱ)由EF =
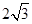 ,EM =" AB" =
,EM =" AB" = ,得FM = 3且
,得FM = 3且 .
.由
 可得FD = 4,从而得CE =1. 8分
可得FD = 4,从而得CE =1. 8分设BC = a,则点B的坐标为(a,
 ,0).又点E、F的坐标分别为(0,
,0).又点E、F的坐标分别为(0, ,1)和(0,0,4),所以
,1)和(0,0,4),所以 ,
, .
.设平面BEF的一个法向量为
 ,则
,则 ,解得一组解为
,解得一组解为 ,所以
,所以 . 10分
. 10分易知平面DEF的一个法向量为
 ,可得
,可得
由于此时
 就是二面角B-EF-D的大小,所以
就是二面角B-EF-D的大小,所以 ,可得
,可得 .
.所以另一边BC的长为
 时,二面角B-EF-D的大小为45°. 12分
时,二面角B-EF-D的大小为45°. 12分
练习册系列答案
相关题目
 ,
, ,则直线
,则直线 的关系是
的关系是 为互不重合的平面,
为互不重合的平面, 为互不重合的直线,给出下列四个命题:
为互不重合的直线,给出下列四个命题: ;
; ;
; ;
; .
. 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.
 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形, ,
, 平面
平面 .
. 是
是 的中点,求证:
的中点,求证:
 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
 中,
中, 两两垂直且相等,过
两两垂直且相等,过 的中点
的中点 作平面
作平面 ∥
∥ ,且
,且 于
于 ,交
,交 的延长线于
的延长线于 .
. 平面
平面 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值.

 和
和 没有公共点,那么
没有公共点,那么