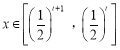题目内容
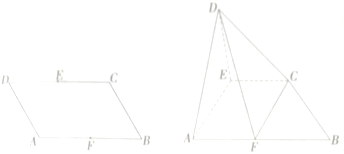
【题目】如图,正方体![]() 中,棱长
中,棱长![]() ,过点
,过点![]() 的平面
的平面![]() 与正方体的面相交,交线围成一个正三角形.
与正方体的面相交,交线围成一个正三角形.

(1)在图中画出这个正三角形(不必说明画法和理由);
(2)平面![]() 将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
【答案】(1)正三角形见解析;(2)体积为![]() ,表面积为
,表面积为![]() .
.
【解析】
试题分析:(1)连接![]() ,则
,则![]() 为所求三角形;(2)截去部分占总体积的六分之一,故较大部分的体积为
为所求三角形;(2)截去部分占总体积的六分之一,故较大部分的体积为![]() .表面积等于一个等边三角形的面积加上三个直角三角形的面积再加上三个正方形的面积,故表面积为
.表面积等于一个等边三角形的面积加上三个直角三角形的面积再加上三个正方形的面积,故表面积为![]() .
.
试题解析:
(1)连接![]() ,则
,则![]() 为所求三角形(做法不唯一),如图所示;……4分
为所求三角形(做法不唯一),如图所示;……4分

(2)平面![]() 将正方体截成三棱锥
将正方体截成三棱锥![]() 和多面体
和多面体![]() 两部分,
两部分,
![]() ,
,
![]() ,
,
因此体积较大的几何体是多面体![]() ,其体积为
,其体积为![]() ,
,
由![]() ,得
,得![]() ,
,
又![]() ,
,![]() ,
,
故多面体![]() 的表面积为
的表面积为![]() .………………10分
.………………10分

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目