题目内容
14.已知R上的奇函数f(x),f(x+2)=f(x),x∈[0,1]时f(x)=1-|2x-1|,定义:f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),n≥2,n∈N,则f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内所有不等实根的和为14.分析 逐次作出f1(x),f2(x),f3(x)的函数图象,观察f3(x)与函数y=$\frac{9}{8(x-1)}$图象交点的横坐标,作图求解即可.
解答 解:∵定义在R上的奇函数f(x),f(x+2)=f(x),
∴f(x)是周期为2的奇函数.
∵x∈[0,1]时,f(x)=1-|2x-1|.
∴函数f1(x)的图象如下图所示:
∵f2(x)=f(f1(x)),
∴函数f2(x)的图象如下图所示: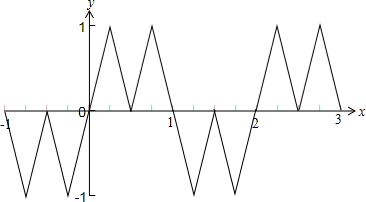
∵f3(x)=f(f2(x)),
∴作函数f3(x)与函数y=$\frac{9}{8(x-1)}$图象如下图所示: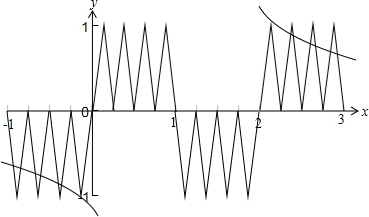
由图可知两函数图象共有14个交点,且两两关于(1,0)点对称,
故f3(x)=$\frac{9}{8(x-1)}$在[-1,3]内所有不等实根的和为14.
故答案为14.
点评 本题考查的知识点是函数的零点个数与方程根的关系,本题图象比较难画,属于难题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.函数f(x)=$\frac{ln(x-1)}{{\sqrt{2-x}}}$的定义域为( )
| A. | (1,2) | B. | (1,2] | C. | (-∞,2] | D. | (1,+∞) |
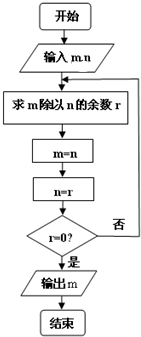 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )