题目内容
求曲线y=
解:y′=(![]() )′=
)′=![]() =
=![]() .
.
由于曲线在M(x0,y0)处的切线斜率为-3,则y′|![]() =
=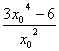 =-3,
=-3,
解得x02=1,即x0=±1.
当x0=1时,y0=![]() =
=![]() =7.
=7.
当x0=-1时,y0=![]() =-7,
=-7,
即M(1,7)或M(-1,-7).
所以所求的切线方程为y-7=-3(x-1),或y+7=-3(x+1),
即3x+y-10=0,或3x+y+10=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
求曲线y=
解:y′=(![]() )′=
)′=![]() =
=![]() .
.
由于曲线在M(x0,y0)处的切线斜率为-3,则y′|![]() =
=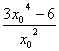 =-3,
=-3,
解得x02=1,即x0=±1.
当x0=1时,y0=![]() =
=![]() =7.
=7.
当x0=-1时,y0=![]() =-7,
=-7,
即M(1,7)或M(-1,-7).
所以所求的切线方程为y-7=-3(x-1),或y+7=-3(x+1),
即3x+y-10=0,或3x+y+10=0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案